How to Derive the Equation of a Parabola Given Two Points and the Axis
When you know two distinct points \((x_1, y_1)\) and \((x_2, y_2)\) and the equation of the axis of symmetry \( x = h \) of a parabola, you can find the equation of the parabola by following these steps:
- A parabola that is parallel to the y-axis has the form $$ y = a(x - h)^2 + k $$ where \( (h, k) \) is the vertex of the parabola.
- Substitute the two known points into the parabola's equation: $$ y_1 = a(x_1 - h)^2 + k $$ $$ y_2 = a(x_2 - h)^2 + k $$ where \( (h,k) \) are the coordinates of the vertex.
- These are two equations with two unknowns (\( a \) and \( k \)). Solve the system to find \( a \) and \( k \) and complete the equation of the parabola.
Alternative Method. Alternatively, if the two points \((x_1, y_1)\) and \((x_2, y_2)\) are not symmetric with respect to the axis \( x=h \), you can find the coordinates of a third point \((x_3, y_3)\) that is symmetric to one of the initial points and determine the equation of the parabola given three points.
Practical Example
Given two points \((2, 3)\) and \((3,5)\) and the axis of symmetry \( x = 1 \) of a parabola, we need to find the equation of the parabola.
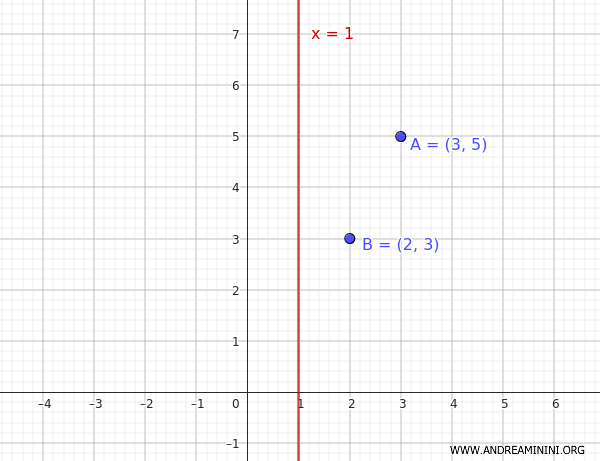
The general form of a parabola parallel to the y-axis is:
$$ y = a(x - h)^2 + k $$
Where \( (h,k) \) is the vertex \( V \) of the parabola.
In this case, the axis of symmetry is \( x=1 \), so \( h = 1 \) because the vertex \( V (h,k)=(1,k) \) lies on this axis.
$$ y = a(x - 1)^2 + k $$
We can create a system of equations by substituting the coordinates of the two known points \((x_1,y_1)=(2, 3)\) and \((x_2,y_2)=(3, 5)\) into the general equation of the parabola:
$$ \begin{cases} y_1 = a(x_1 - 1)^2 + k \\ \\ y_2 = a(x_2 - 1)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a(2 - 1)^2 + k \\ \\ 5 = a(3 - 1)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a(1)^2 + k \\ \\ 5 = a(2)^2 + k \end{cases} $$
$$ \begin{cases} 3 = a + k \\ \\ 5 = 4a + k \end{cases} $$
This system has two equations with two unknowns.
We can solve it using substitution to find the values of \( a \) and \( k \):
$$ \begin{cases} k = 3 - a \\ \\ 5 = 4a + k \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 5 = 4a + (3-a) \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 5 = 3a + 3 \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ 3a = 2 \end{cases} $$
$$ \begin{cases} k = 3 - a \\ \\ a = \frac{2}{3} \end{cases} $$
$$ \begin{cases} k = 3 - \frac{2}{3} \\ \\ a = \frac{2}{3} \end{cases} $$
$$ \begin{cases} k = \frac{9-2}{3} \\ \\ a = \frac{2}{3} \end{cases} $$
$$ \begin{cases} k = \frac{7}{3} \\ \\ a = \frac{2}{3} \end{cases} $$
With \( k \) found, we know the vertex coordinates \( (h,k)=(1, \frac{7}{3}) \).
Since we also know \( a = \frac{2}{3} \) and \( h =1 \), we can write the general equation of the parabola:
$$ y = a(x - h)^2 + k $$
$$ y = \frac{2}{3} \cdot (x - 1)^2 + \frac{7}{3} $$
Here is the graphical representation:
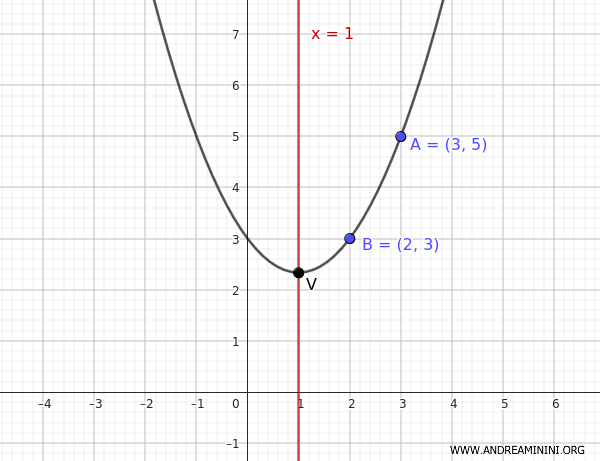
Alternative Solution
We know the coordinates of two points \( (2, 3)\) and \((3,5)\) and the axis of symmetry \( x = 1 \) of the parabola.

The two points are not symmetric to each other with respect to the axis of symmetry \( x=1 \).
We can choose one of the points, for example, \( B (2,3) \), and calculate a third point \( C(0,3) \) that is symmetric with respect to the axis \( x=1 \).
When the axis of symmetry is parallel to the y-axis according to axial symmetry, a point is symmetric to another if:
$$ \begin{cases} x' = 2h - x \\ \\ y' = y \end{cases} $$
In this case, the axis of symmetry is \( h=1 \), and the coordinates of point B are \( x=2 \) and \( y=3 \).
$$ \begin{cases} x' = 2 \cdot 1 - 2 \\ \\ y' = 3 \end{cases} $$
$$ \begin{cases} x' = 0 \\ \\ y' = 3 \end{cases} $$
So, the coordinates of the third point are \( C(0,3) \).
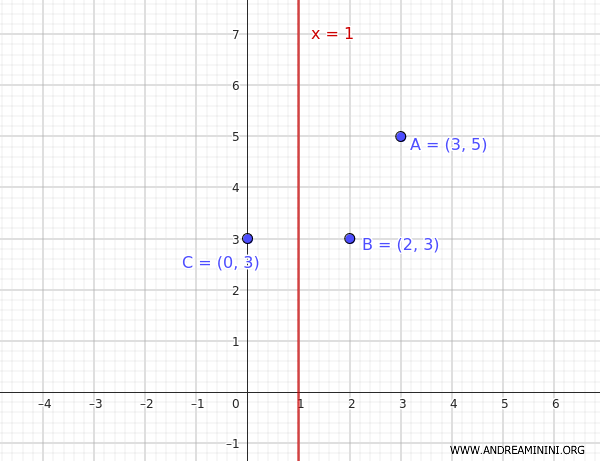
Now, knowing the coordinates of three points \( A(3,5) \), \( B(2,3) \), and \( C(0,3) \), we can set up a system of three equations:
$$ \begin{cases} ax_1^2 + bx_1 + c = y_1 \\ \\ ax_2^2 + bx_2 + c = y_2 \\ \\ ax_3^2 + bx_3 + c = y_3 \end{cases} $$
Substitute the coordinates of each known point into the equations:
$$ \begin{cases} a \cdot 3^2 + b \cdot 3 + c = 5 \\ \\ a \cdot 2^2 + b \cdot 2 + c = 3 \\ \\ a \cdot 0 ^2 + b \cdot 0 + c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b + c = 5 \\ \\ 4a + 2b + c = 3 \\ \\ c = 3 \end{cases} $$
Now, solve the system to find the coefficients \( a \), \( b \), and \( c \):
$$ \begin{cases} 9a + 3b + 3 = 5 \\ \\ 4a + 2b + 3 = 3 \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ 4a + 2b = 0 \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ b = \frac{-4a}{2} \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3b = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a + 3(-2a) = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 9a - 6a = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} 3a = 2 \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -2a \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -2 \cdot \frac{2}{3} \\ \\ c = 3 \end{cases} $$
$$ \begin{cases} a = \frac{2}{3} \\ \\ b = -\frac{4}{3} \\ \\ c = 3 \end{cases} $$
We have found the coefficients \( a \), \( b \), and \( c \) which can be substituted into the equation of the parabola:
$$ y = ax^2 + bx + c $$
$$ y = \frac{2}{3} x^2 - \frac{4}{3}x + 3 $$
This gives us the equation of the parabola.
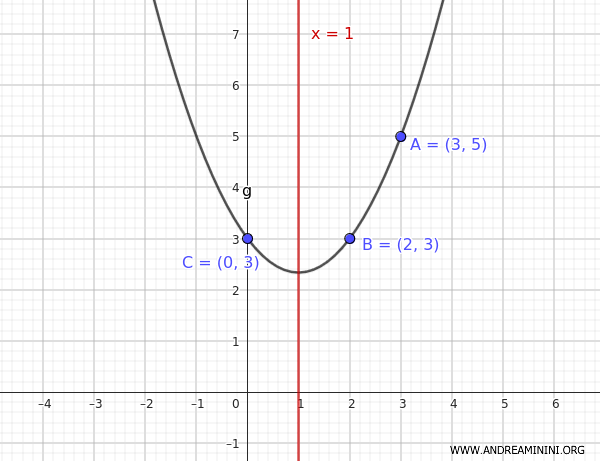
And so on.
