Archimedes' Theorem on the Area of a Parabolic Segment
The area \( S \) of a parabolic segment, which is the region bounded by a parabola and a chord AB that is not the axis of symmetry, is equal to two-thirds of the area \( A \) of the rectangle constructed on the tangent line to the parabola, parallel to the chord. $$ S = \frac{2}{3} \times A $$
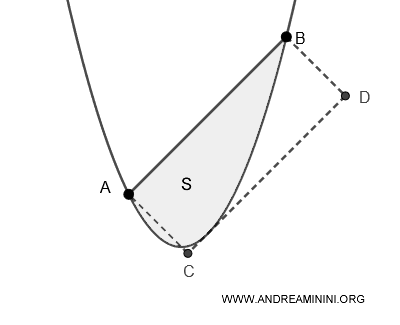
Alternatively, the area of the parabolic segment can also be described as four-thirds of the area of the inscribed triangle ABC within the segment, where the base is the chord AB and the opposite vertex C is the point where the tangent line to the parabola, parallel to the chord, touches the curve.
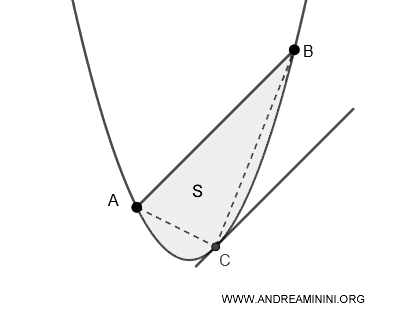
If the inscribed triangle has an area \( A \), then the area \( S \) of the parabolic segment is given by:
$$ S = \frac{4}{3} \times A $$
This formula is remarkably accurate for its time, showcasing the brilliance of Archimedes' geometric methods.
Note: To determine the area of the parabolic segment precisely, one would typically integrate the function describing the parabola. However, Archimedes' theorem offers an alternative numerical method that doesn't require the tools of calculus.
Practical Example
Let's consider a simple parabola:
$$ y = x^2 $$
Next, draw a chord AB with endpoints at A(-1, 1) and B(2, 4).
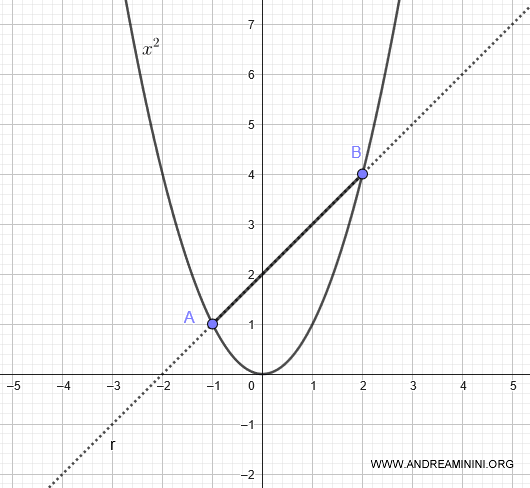
We need to calculate the area of the region beneath the chord AB within the parabola.
To do this, we’ll use Archimedes' method. First, we find the line parallel to segment AB that is also tangent to the parabola.
The segment AB lies on the line r:
$$ y = x + 2 $$
The family of lines parallel to line r is given by:
$$ y = mx + q $$
The points of intersection between the parabola \( y = x^2 \) and the family of lines \( y = mx + q \) are determined by:
$$ x^2 = mx + q $$
Among these, we need to find the line that is tangent to the parabola.
We rewrite the equation of the family of lines in the general form:
$$ y - mx - q = 0 $$
For the line to be tangent, the discriminant of this equation must be zero:
$$ \Delta = 0 $$
The discriminant is given by:
$$ \Delta = b^2 - 4ac = 0 $$
In this case, the line is \( y - mx - q = 0 \), where \( a = 1 \), \( b = -m \), and \( c = -q \).
$$ \Delta = (-m)^2 - 4 \cdot 1 \cdot (-q) = 0 $$
$$ m^2 + 4q = 0 $$
From this, we find \( q \):
$$ q = - \frac{m^2}{4} $$
So, the tangent line to the parabola that is parallel to chord AB is:
$$ y = mx + q $$
$$ y = mx - \frac{m^2}{4} $$
The slope \( m \) of the line \( y = x + 2 \), which passes through chord AB, is \( m = 1 \).
$$ y = 1 \cdot x - \frac{1^2}{4} $$
$$ y = x - \frac{1}{4} $$
This final equation represents the tangent line to the parabola \( y = x^2 \) that is parallel to chord AB.
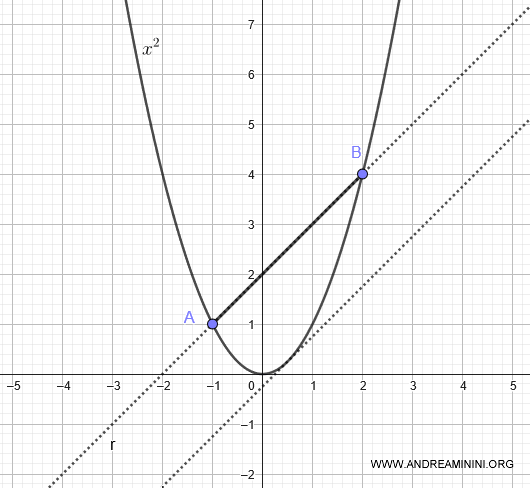
We draw two perpendicular segments from the line r to the tangent line, with endpoints at points A and B.
This creates a rectangle ABCD.
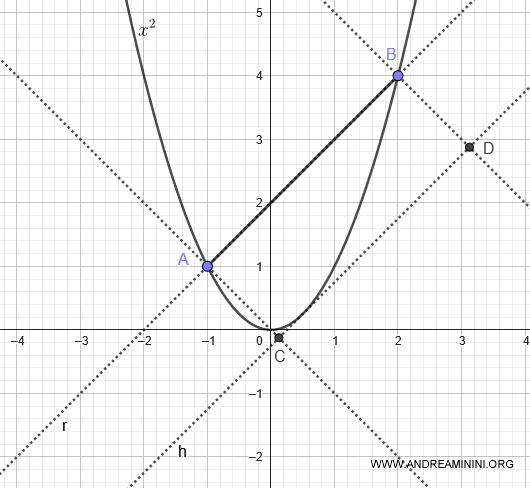
According to Archimedes' theorem, two-thirds of the area of rectangle ABCD is equal to the area under the parabola beneath chord AB.
To measure the length of side AB of the rectangle, we calculate the distance between points A and B:
$$ \overline{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $$
Where \( A(-1, 1) \) and \( B(2, 4) \).
$$ \overline{AB} = \sqrt{(2 - (-1))^2 + (4 - 1)^2} $$
$$ \overline{AB} = \sqrt{3^2 + 3^2} $$
$$ \overline{AB} = \sqrt{9 + 9} $$
$$ \overline{AB} = \sqrt{18} $$
To measure the length of side AC of the rectangle, we calculate the distance between point A(-1,1) and the tangent line \( y = x - \frac{1}{4} \).
$$ \overline{AC} = \frac{|ax + by + c|}{\sqrt{a^2 + b^2}} $$
Knowing that the tangent line is \( y = x - \frac{1}{4} \), or \( -x + y + \frac{1}{4} = 0 \), we find the coefficients \( a = -1 \), \( b = 1 \), and \( c = \frac{1}{4} \).
$$ \overline{AC} = \frac{|-1 \cdot x + 1 \cdot y + \frac{1}{4}|}{\sqrt{(-1)^2 + 1^2}} $$
$$ \overline{AC} = \frac{|-x + y + \frac{1}{4}|}{\sqrt{2}} $$
Substituting \( x \) and \( y \) with the coordinates of point A(-1,1):
$$ \overline{AC} = \frac{|-(-1) + 1 + \frac{1}{4}|}{\sqrt{2}} $$
$$ \overline{AC} = \frac{|1 + 1 + \frac{1}{4}|}{\sqrt{2}} $$
$$ \overline{AC} = \frac{| \frac{4 + 4 + 1}{4}|}{\sqrt{2}} $$
$$ \overline{AC} = \frac{| \frac{9}{4}|}{\sqrt{2}} $$
$$ \overline{AC} = \frac{9}{4} \cdot \frac{1}{\sqrt{2}} $$
$$ \overline{AC} = \frac{9}{4 \cdot \sqrt{2}} $$
Now we can calculate the area \( A \) of rectangle ABCD:
$$ A = \overline{AB} \cdot \overline{AC} $$
$$ A = \sqrt{18} \cdot \frac{9}{4 \cdot \sqrt{2}} $$
$$ A = \sqrt{2 \cdot 3^2} \cdot \frac{9}{4 \cdot \sqrt{2}} $$
$$ A = 3 \cdot \sqrt{2} \cdot \frac{9}{4 \cdot \sqrt{2}} $$
$$ A = 3 \cdot \frac{9}{4} $$
$$ A = \frac{27}{4} $$
According to Archimedes' theorem, the area under chord AB is equal to two-thirds of the area of rectangle ABCD:
$$ S = \frac{2}{3} \cdot A $$
$$ S = \frac{2}{3} \cdot \frac{27}{4} $$
$$ S = \frac{1}{3} \cdot \frac{27}{2} $$
$$ S = \frac{27}{6} $$
$$ S \approx 4.5 $$
Therefore, the area between chord AB and the parabola is 4.5.
Verification: To verify this result, we can calculate the area between the chord AB and the x-axis.
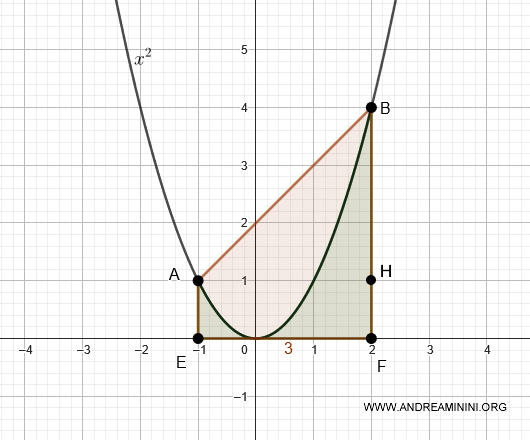
The area AEFB consists of the area of triangle AHF with a base of 3 and a height of 3, plus the area of rectangle AEFH with a base of 3 and a height of 1.
$$ Area(AEFB) = Area(AHF) + Area(AEFH) $$
$$ Area(AEFB) = \frac{3 \cdot 3}{2} + 3 \cdot 1 $$
$$ Area(AEFB) = \frac{9}{2} + 3 $$
$$ Area(AEFB) = \frac{9 + 6}{2} $$
$$ Area(AEFB) = \frac{15}{2} $$
$$ Area(AEFB) = 7.5 $$
The area between the parabola and the x-axis (in green) is obtained by integrating the function \( x^2 \) between the limits \( a = -1 \) and \( b = 2 \).
$$ \int_a^b x^2 \, dx $$
Where \( a = -1 \) and \( b = 2 \) are the x-axis limits of chord AB.
$$ \int_{-1}^2 x^2 \, dx $$
The integral of \( x^2 \) is \( \frac{x^3}{3} \), so the integral is:
$$ \int_{-1}^2 x^2 \, dx = \left| \frac{x^3}{3}\right|_{-1}^{2} = \frac{2^3}{3} - \frac{(-1)^3}{3} = \frac{8}{3} + \frac{1}{3} = \frac{9}{3} = 3 $$
Thus, the area under the parabola is 3.
$$ \int_{-1}^2 x^2 \, dx = 3 $$
The area \( S \) between the chord AB and the parabola \( x^2 \) is equal to the difference between the area AEFB and the area under the parabola (i.e., the integral):
$$ S = Area(AEFB) - \int_{-1}^2 x^2 \, dx $$
The area AEFB is 7.5, while the integral is 3.
$$ S = 7.5 - 3 $$
$$ S = 4.5 $$
The final result matches the one obtained using Archimedes' method: the area between the chord AB and the parabola is 4.5.
Proof
Consider a parabolic segment, which is the region bounded by a parabola and a chord AB connecting two points on the parabola.
Construct an inscribed triangle ABC with the chord AB as the base and the vertex at the point C on the parabola that lies on the perpendicular drawn from the midpoint M of the chord AB.
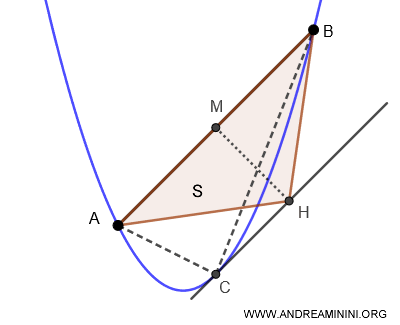
To verify the result, Archimedes used an approximation method that we would now call the "method of exhaustion," a precursor to integral calculus.
He divided the parabolic segment into a series of smaller triangles, showing that the total area of these triangles approaches the true area of the parabolic segment.
And so on.
