Isosceles Trapezoid Theorem

In an isosceles trapezoid, the angles adjacent to each base are congruent.

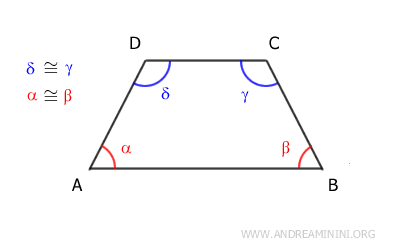
For example, in the isosceles trapezoid ABCD, angles alpha and beta are congruent because they are adjacent to the longer base AB.

$$ \alpha \cong \beta $$

Likewise, angles gamma and delta are congruent because they are adjacent to the shorter base CD.

$$ \gamma \cong \delta $$

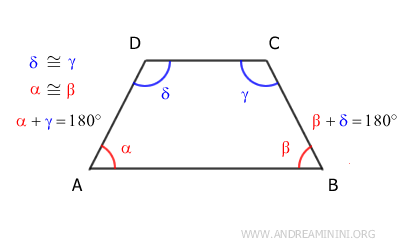
Corollary: In an isosceles trapezoid, opposite angles are supplementary, meaning their sum equals 180°. $$ \alpha + \gamma = 180° $$ $$ \beta + \delta = 180° $$

Proof

Let’s consider an isosceles trapezoid ABDC.

Since it's an isosceles trapezoid, the non-parallel sides are congruent, AD≅CB.

An isosceles trapezoid can be divided into three shapes: two right triangles (ADE, BCF) and a quadrilateral, which could be either a square or a rectangle (BCDE).

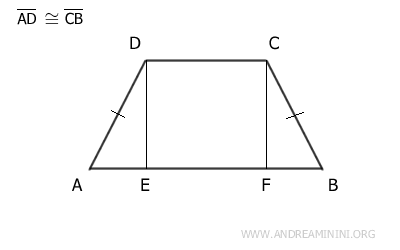
The quadrilateral BCDE has four right angles by definition, whether it's a rectangle or a square.

Additionally, the sides DE and CF of the quadrilateral are opposite and therefore congruent, DE≅CF.

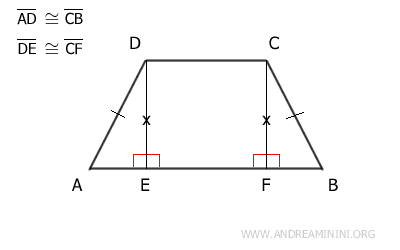
According to the right triangle congruence criterion, triangles ADE and BCF are congruent (ADE≅BCF) because they have congruent hypotenuses (AD≅CB) and congruent legs (DE≅CF).

As a result, since the triangles ADE and BCF are congruent, their corresponding angles are congruent as well.

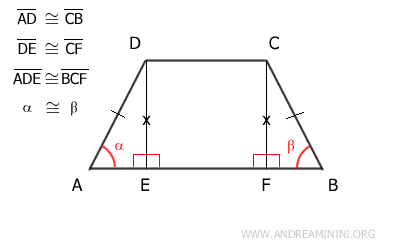
In particular, it’s crucial to note that angles α≅β are congruent.

$$ \alpha = \beta $$

Next, we apply the parallel lines theorem, considering side AD as a transversal intersecting the parallel lines AB and CD.

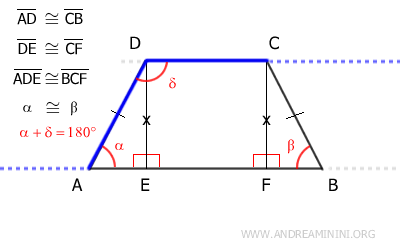
According to the parallel lines theorem, corresponding angles (alpha and delta) are supplementary, meaning their sum equals 180°.

$$ \alpha + \delta = 180° $$

Now, consider side BC as a transversal of lines AB and CD.

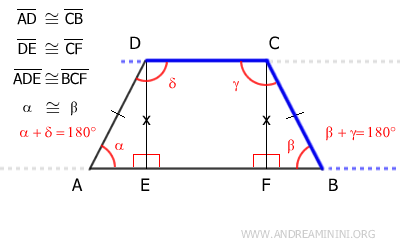
For the same reason, corresponding angles beta and gamma are supplementary, β+γ=180°.

$$ \beta + \gamma = 180° $$

Knowing that α≅β, we can deduce that γ≅δ as well, since they are supplementary angles to congruent angles.

$$ \alpha + \delta \cong \beta + \gamma = 180° $$

$$ \alpha + \delta \cong \beta + \gamma $$

$$ \alpha + \delta - \beta \cong \gamma $$

$$ \delta \cong \gamma $$

In conclusion, the angles adjacent to each base are congruent in an isosceles trapezoid.

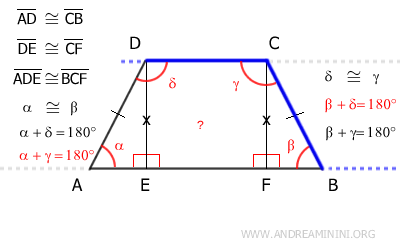
Therefore, knowing that the angles adjacent to the non-parallel sides are supplementary (180°), we conclude that in an isosceles trapezoid, opposite angles are supplementary (α+γ=180° and β+δ=180°).

Converse of the Isosceles Trapezoid Theorem

If a trapezoid has congruent angles adjacent to one of its bases, then it is an isosceles trapezoid.

Proof

As an initial assumption, let's consider a trapezoid ABCD with congruent angles adjacent to one of its bases.

For example, the angles α≅β adjacent to base AB are congruent.

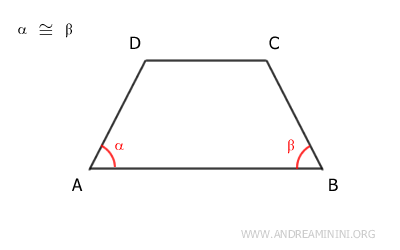
We don’t yet know what type of trapezoid this is, but we do know that its bases are parallel, AB||CD.

As a result, the heights of the trapezoid DE and CF are congruent, DE≅CF, and are perpendicular to the bases, forming right angles (90°) with base AB.

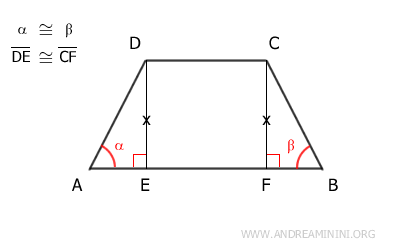
These heights create two right triangles, ADE and BCF, within the trapezoid.

The two triangles ADE≅BCF are congruent by the second congruence criterion, as they share a congruent side DE≅CF, two congruent angles α≅β, and a right angle (90°).

Therefore, the congruent triangles ADE≅BCF have all corresponding sides and angles congruent.

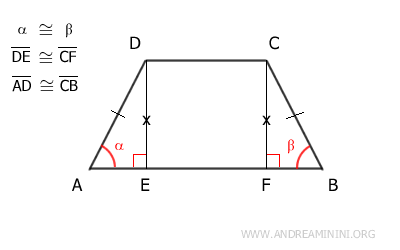
In this context, it is particularly important to note that the hypotenuses AD≅BC are congruent, as they are also the non-parallel sides of the trapezoid.

In conclusion, since the trapezoid has congruent non-parallel sides AD≅BC, it is indeed an isosceles trapezoid.

And so on.