Isosceles Trapezoid

An isosceles trapezoid is a trapezoid with two congruent non-parallel sides, meaning they are equal in length.

The isosceles trapezoid belongs to the trapezoid family, characterized by two parallel sides that are not equal in length, known as the longer base (AB) and the shorter base (CD).

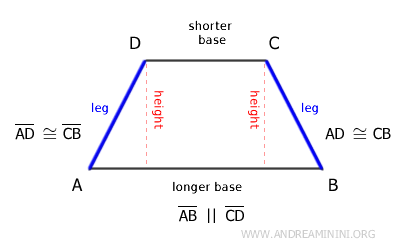
What distinguishes it from other trapezoids is that it has two non-parallel sides of equal length.

An isosceles trapezoid has the following key properties:

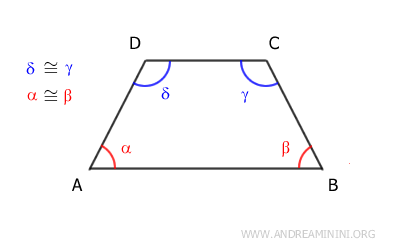
• The angles adjacent to the longer base are congruent (e.g., α≅β).
• The angles adjacent to the shorter base are also congruent (e.g., γ≅δ).
  
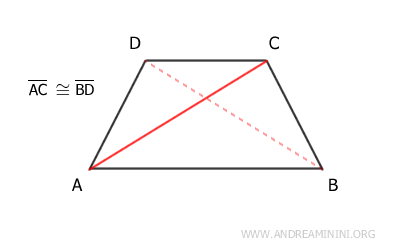
• The diagonals are congruent.
  

Formulas for the Isosceles Trapezoid

Here are some important formulas related to the isosceles trapezoid:

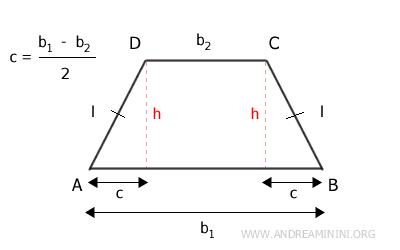
• Non-parallel Side
  The length of each non-parallel side (l) can be calculated using the Pythagorean theorem. It is the square root of the sum of the square of half the difference between the longer and shorter bases, c=(b₁-b₂)/2, plus the square of the height (h). $$ l = \sqrt{c^2 + h^2} $$
• Height
  The height (h) of the isosceles trapezoid can be derived from the formula for the non-parallel side. $$ h = \sqrt{l^2 - c^2} $$ Here, l is the length of a non-parallel side of the isosceles trapezoid, and c is half the difference between the longer and shorter bases, c=(b₁-b₂)/2.

Isosceles Trapezoid Theorem

In an isosceles trapezoid, the angles adjacent to each base are congruent.

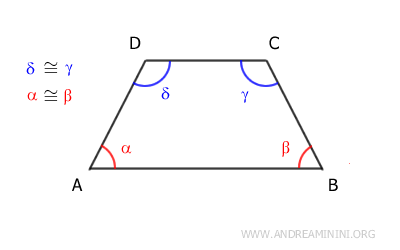
From this, we can infer that the opposite angles in an isosceles trapezoid are supplementary angles, meaning their sum is equal to 180°.

$$ \alpha + \gamma = 180° $$

$$ \beta + \delta = 180° $$

The converse theorem is also true:

If the angles adjacent to each base in a trapezoid are congruent, then the trapezoid is isosceles.

And so on...