Right-Angled Trapezoid

A right-angled trapezoid is a type of trapezoid where one side is perpendicular to the bases.

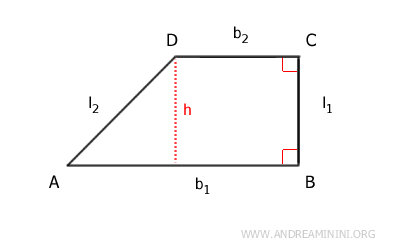
It’s a flat geometric shape that belongs to the quadrilateral family.

The defining characteristic of a right-angled trapezoid is that it has two parallel sides, called the larger base and the smaller base, with one of the angles adjacent to the bases being exactly 90 degrees.

This right angle is what gives the trapezoid its name.

The Bases and the Height

A right-angled trapezoid has two bases of different lengths.

The larger base (b₁) is the longer side, while the smaller base (b₂) is the shorter side.

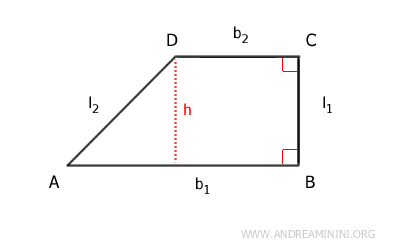
The two non-parallel sides, l₁ and l₂, are not parallel. One of these sides (l₁) forms a right angle with the bases.

The perpendicular distance between the two bases is known as the height of the trapezoid.

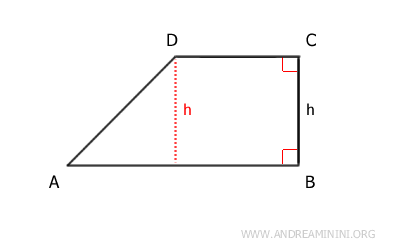
In a right-angled trapezoid, the height is the same as the oblique side that is perpendicular to the bases.

Formulas

Key formulas for the right-angled trapezoid:

• Perimeter
  The perimeter P of a right-angled trapezoid is the sum of the lengths of its four sides: $$ P = l_1 + l_2 + b_1 + b_2 $$
• Area
  The area of a right-angled trapezoid is calculated like any other trapezoid: it’s half the product of the sum of the bases (b₁ + b₂) and the height (h). $$ A = \frac{(b_1 + b_2) \cdot h}{2} $$ Here, b₁ is the smaller base, b₂ is the larger base, and h is the height of the trapezoid.
• Oblique Side
  The length of the oblique side (l₂) can be determined using the Pythagorean theorem. It’s the square root of the sum of the square of the difference between the larger and smaller bases (b₁ - b₂) plus the square of the height (h). $$ l_2 = \sqrt{(b_1 - b_2)^2 + h^2} $$
• Height
  The height (h) of the right-angled trapezoid can also be found using the Pythagorean theorem: $$ h = \sqrt{l_2^2 - (b_1 - b_2)^2} $$ Where l₂ is the oblique side of the trapezoid.

And so on...