Trapezoid Area

The area of a trapezoid is calculated by multiplying the height (h) by the average of the lengths of its two bases, (b₁ + b₂) / 2. $$ A = \frac{(b_1+b_2) \cdot h}{2} $$ Here, b₁ is the longer base, b₂ is the shorter base, and h is the height of the trapezoid, which is the perpendicular distance between the two bases.

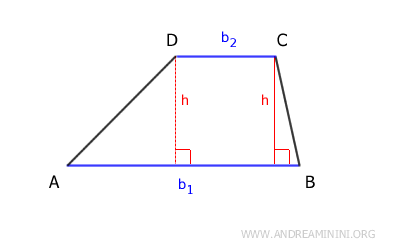
A trapezoid is a four-sided geometric figure with at least two parallel sides, referred to as the bases.

The area of the trapezoid represents the size of the surface enclosed within this shape.

A Practical Example

Let's say we have a trapezoid with a longer base of 8 cm, a shorter base of 5 cm, and a height of 4 cm.

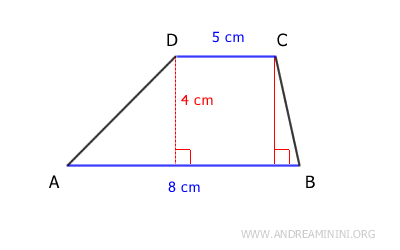
Using the formula:

$$ A = \frac{(8+5) \cdot 4}{2} $$

$$ A = \frac{13 \ \text{cm} \ \cdot 4 \ \text{cm} }{2} $$

$$ A = \frac{52 \ \text{cm}^2 }{2} $$

$$ A = 26 \ \text{cm}^2 $$

So, the area of the trapezoid in this example is 26 cm².

The Proof

If we draw a perpendicular line (h) from the ends of the shorter base to the longer base of the trapezoid, it divides the shape into two right triangles and a rectangle in the center.

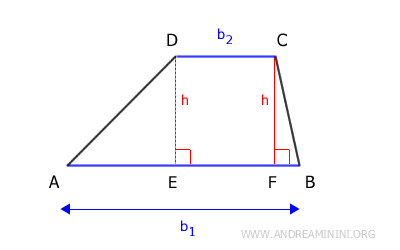
Thus, the area of the trapezoid can be considered the sum of the areas of two triangles (AED and BCF) and the rectangle (EFCD).

The total area of these three shapes is the area of the trapezoid (A).

$$ A = \frac{ \overline{AE} \cdot h }{2} + \frac{ \overline{BF} \cdot h }{2} + h \cdot \overline{EF} $$

Here, AE·h/2 represents the area of the first triangle, BF·h/2 represents the area of the second triangle, and BF·h represents the area of the rectangle.

By factoring out the height (h), we get:

$$ A = h \cdot \left( \frac{ \ \overline{AE} }{2} + \frac{ \overline{BF} }{2} + \overline{EF} \right) $$

$$ A = h \cdot \left( \frac{ \ \overline{AE} + \overline{BF} + 2 \overline{EF} }{2} \right) $$

We can rewrite 2EF = EF + CD.

$$ A = h \cdot \left( \frac{ \ \overline{AE} + \overline{BF} + \overline{EF} + \overline{CD} }{2} \right) $$

The sum of the lengths of the segments AE + BF + EF = b₁ equals the longer base.

$$ A = h \cdot \frac{ ( b_1 + \overline{CD} ) }{2} $$

Knowing that the segment CD = b₂ represents the length of the shorter base, we have:

$$ A = h \cdot \frac{ ( b_1 + b_2 ) }{2} $$

This final result is the formula we set out to prove.

An Alternative Proof

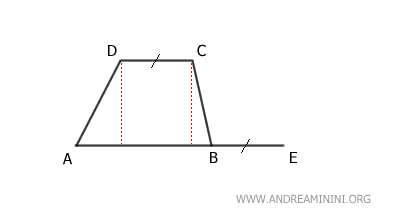
Consider a trapezoid ABCD.

Extend the longer base AB by adding a segment at E, such that BE is congruent to CD, the shorter base.

Next, extend the shorter base CD by adding a segment CF=AB at point D, making it congruent with the longer base.

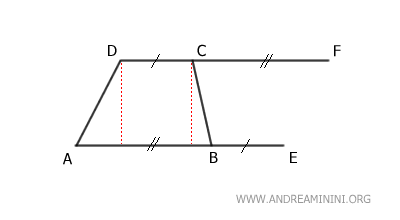
Draw the segment EF to connect points E and F.

This transforms the trapezoid into a parallelogram ADFE, which consists of two trapezoids: ABCD and BEFC.

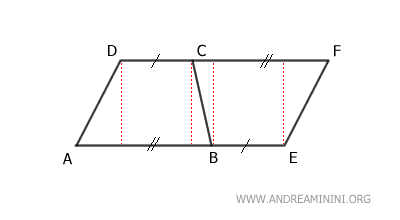
The trapezoids ABCD and BEFC are congruent because they have the same sides in the same order.

Therefore, trapezoid ABCD is equivalent to half of the parallelogram ADFE.

The area of the parallelogram is calculated by multiplying the base by the height.

$$ A_p = \overline{AE} \cdot h $$

The segment AE is composed of AB = b₁ and BE = b₂, which are the bases of the original trapezoid.

$$ A_p = ( \overline{AB} + \overline{BE} ) \cdot h $$

$$ A_p = ( b_1 + b_2 ) \cdot h $$

Since the trapezoid is half of the parallelogram, we conclude that the area of the trapezoid is half the area of the parallelogram.

$$ A = \frac{A_p}{2 } $$

$$ A = \frac{ ( b_1 + b_2 ) \cdot h}{2 } $$

This method also proves the formula for calculating the area of a trapezoid.

And there you have it!