Midsegment Theorem for a Trapezoid
In a trapezoid, the segment EF that connects the midpoints E and F of the non-parallel sides is parallel to the bases and has a length equal to the average of the lengths of the two bases. $$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
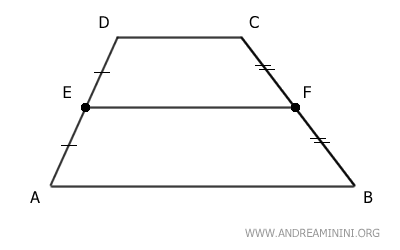
A Practical Example
Let's consider the trapezoid ABCD.
The non-parallel sides AD and BC have their midpoints at E and F, respectively.
The segment EF, which connects these midpoints, is parallel to the bases AB and CD of the trapezoid.
Furthermore, the length of segment EF is equal to half the sum of the lengths of the two bases: (AB + CD)/2.
$$ \overline{EF} = \frac{\overline{CD} + \overline{AB} }{2} $$
The Proof
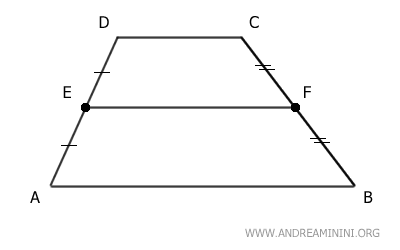
Now, let's examine the trapezoid ABCD.
Point E is the midpoint of the non-parallel side AD.
Since E is the midpoint, it divides AD into two congruent segments, AE ≅ DE.
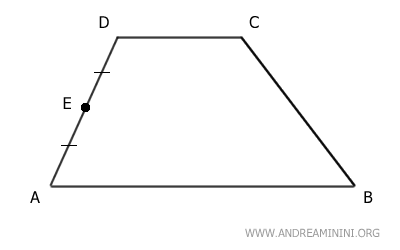
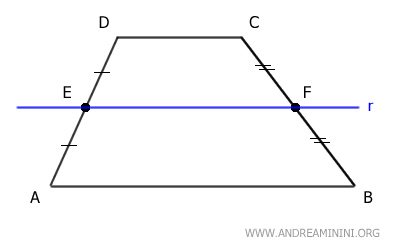
Next, draw a line r parallel to the base AB that passes through the midpoint E of side AD.
According to the Parallel Lines Theorem, line r intersects side BC at its midpoint F, dividing BC into two congruent segments, BF ≅ CF.
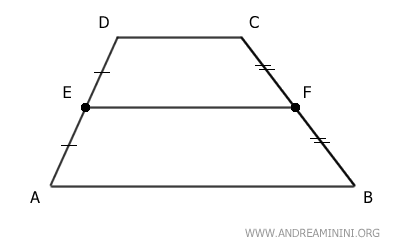
Now, consider the segment EF, which connects the midpoints of the non-parallel sides AD and BC.
Next, draw the diagonal AC, which divides the trapezoid into two triangles and intersects segment EF at point G.
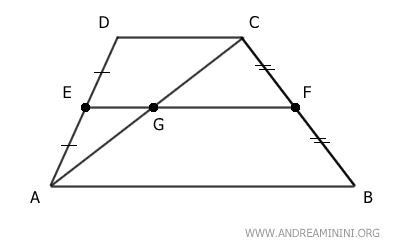
Let's analyze triangle ACD.
Segment EG, with one endpoint at the midpoint E of side AD, is parallel to side CD of triangle ACD.
Therefore, according to the Triangle Midsegment Theorem, point G is the midpoint of the remaining side AC, and segment EG is half the length of side CD.
$$ \overline{EG} = \frac{ \overline{CD} }{2} $$
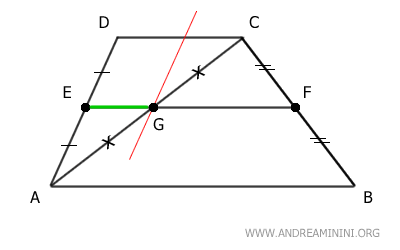
Now, let's consider triangle ABC.
Segment FG connects the midpoints G of side AC and F of side BC.
According to the Triangle Midsegment Theorem, segment FG is parallel to and half the length of side AB.
$$ \overline{FG} = \frac{ \overline{AB} }{2} $$
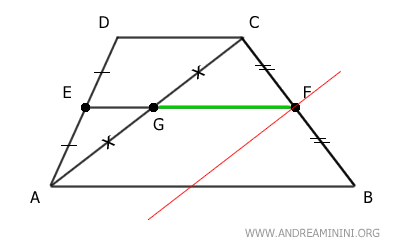
To summarize, the segment that connects the midpoints E and F of the non-parallel sides of trapezoid AD and BC is composed of segments EG and FG.
$$ \overline{EF} = \overline{EG} + \overline{FG} $$
Both segments, EG and FG, are parallel to the bases of the trapezoid, AB and CD.
Therefore, segment EF is parallel to the bases of the trapezoid.
Moreover, since EG = CD/2 and FG = AB/2, the length of segment EF is equal to the average of the lengths of the bases of the trapezoid.
$$ \overline{EF} = \overline{EG} + \overline{FG} = \frac{ \overline{CD} }{2} + \frac{ \overline{AB} }{2} = \frac{\overline{CD} + \overline{AB} }{2} $$
This completes the proof of the midsegment theorem for a trapezoid.
And so on.
