Calculating the Area of a Rectangle
The area of a rectangle is calculated by multiplying the base by the height: $$ A = b \ × \ h $$ 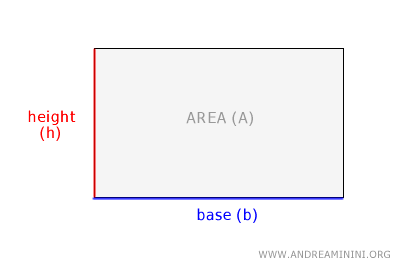
Understanding and calculating the area of a rectangle is a simple and straightforward concept.
To help visualize this, imagine a rectangle as a room. The area of this room (or rectangle) is determined by multiplying its length by its width.
For example, if the room is 5 meters long and 3 meters wide, to find the area, you would multiply the 5 meters (length) by the 3 meters (width).
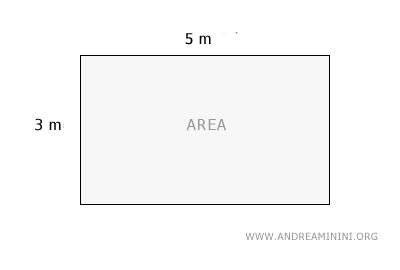
Thus, the area of the rectangle is 15 square meters. This calculation is practical, for instance, when figuring out how much flooring is needed to cover the entire surface of the room.
$$ A = 5 \ meters \ × \ 3 \ meters = 15 \ square \ meters \ (sqm) $$
In more formal terms, you can write:
$$ A = 5 \ m × 3 \ m = 15 \ m^2 $$
In general, if we denote the length by L and the width by W, the area A is calculated using the formula A = L × W.
$$ Area = Length \ × \ Width $$
This method of calculation is straightforward and universally applicable to any rectangle.
Proof of the Formula
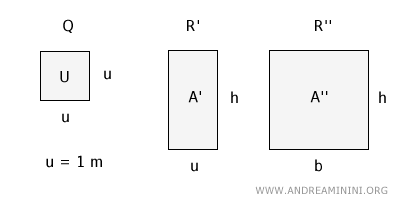
To prove this formula, let's consider a square Q with a side length equal to the unit of measurement u = 1 meter.

This square represents 1 square meter, which is the standard unit for measuring area U = 1 sqm.
$$ U = 1 \ sqm = 1 \ m^2 $$
Now, let's consider two rectangles: the first rectangle R' has a width equal to the unit of measurement (u = 1 m) and a height h.
The second rectangle R'' has a width of b (chosen arbitrarily) and the same height h as the first rectangle.
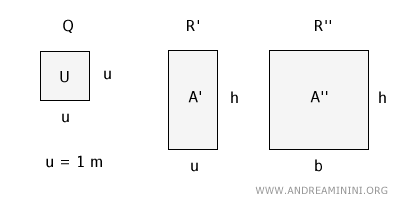
$$ A' = \frac{h \cdot m^2}{1 \ m} $$
These two rectangles, R' and R'', have areas A' and A'' respectively, which are not yet known.
However, since they have the same height h, the only difference is their width. Therefore, their areas are directly proportional to their widths.
$$ A'' : A' = b:u $$
We know the width of rectangle R' because, by assumption, it equals the unit of measurement u = 1 m.
$$ A'' : A' = b:1 \ m $$
By applying the properties of proportions, we can deduce that the area A'' of rectangle R'' is equal to the product of the area A' of rectangle R' and the base (b).
$$ A'' = b \cdot A' \cdot m $$
However, we still need to determine the value of the area A' of rectangle R'.
To do this, let's take a step back and compare rectangle R' with square Q.
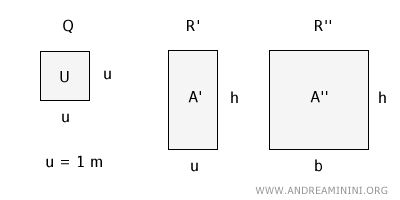
Rectangle R' and square Q have the same base (u = 1 m), so their areas are directly proportional to their heights.
$$ A' : U = h : u $$
Since we know U = 1 sqm and u = 1 meter:
$$ A' : 1 \ m^2 = h : 1 \ m $$
Using the properties of proportions:
$$ \frac{A'}{1 \ m^2} = \frac{h}{1 \ m} $$
By the invariant property of equations, multiply both sides by 1 m2:
$$ \frac{A'}{1 \ m^2} \cdot m^2 = \frac{h}{1 \ m} \cdot m^2 $$
$$ A' = h \cdot m $$
Thus, we find that A' = h meters
$$ A' = h \cdot m $$
Once we have found the area of rectangle R', which is A' = h·m, we can substitute it into the previous proportion.
$$ A'' = b \cdot A' \cdot m $$
$$ A'' = b \cdot ( h \cdot m ) \cdot m $$
$$ A'' = b \cdot h \cdot m^2 $$
In other words:
$$ A'' = b \cdot h \ sqm $$
This demonstrates that the area of rectangle R'' is equal to the product of its base (b) and height (h), and is measured in square meters.
And so forth.
