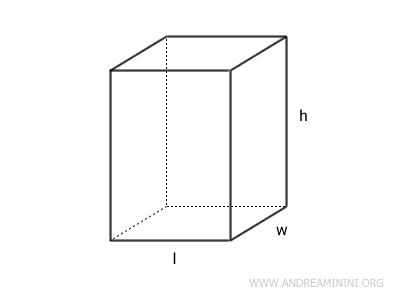
Volume of a Rectangular Prism

The volume V of a rectangular prism is found by multiplying the area of its base A_B by its height h: $$ V = A_B \cdot h $$. Alternatively, since $ A_B = l \cdot w $, the volume can be expressed as the product of the prism’s length (l), width (w), and height (h): $$ V = l \cdot w \cdot h $$

Proof

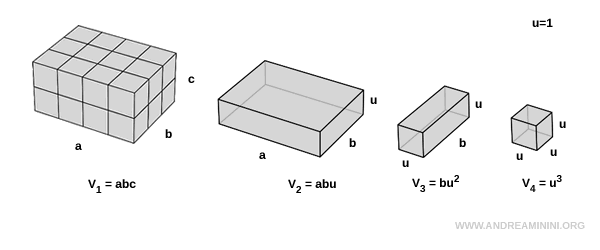
Let’s consider four rectangular prisms and assume a unit of measurement $ u = 1 $.

The final solid is a unit cube with a volume of $ V_4 = u^3 $.

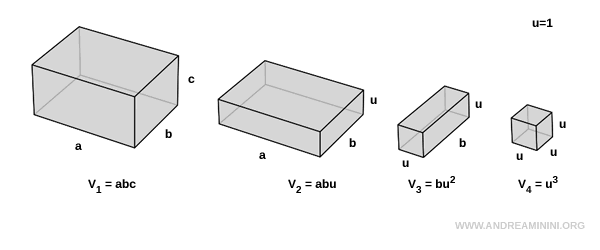
We aim to prove that the volume of the first prism is given by $ V_1 = abc $.

We’ll use a constructive approach. Starting with a unit cube, we observe that the volume of a solid can be determined by counting how many unit cubes ($ u = 1 $) it contains.

The first and second prisms share the same base area $ a \cdot b $, but have different heights ($ c $ in the first, and $ u $ in the second):

$$ V_1 = a \cdot b \cdot c $$

$$ V_2 = a \cdot b \cdot u $$

According to a property of prisms, when the base area is the same, volumes are proportional to their heights:

$$ V_1 : V_2 = c : u $$

Which leads to:

$$ V_1 = \frac{c}{u} \cdot V_2 $$

Since $ u = 1 $, this simplifies to:

$$ V_1 = c \cdot V_2 $$

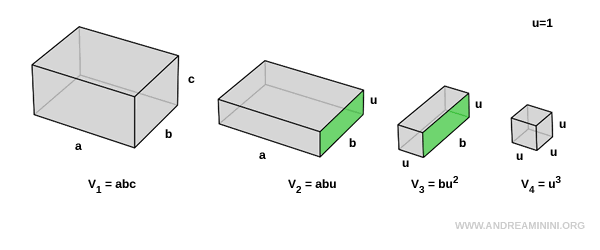
The second and third prisms share a face of area $ b \cdot u $, but differ in length ( $ a $ vs $ u $ ):

$$ V_2 = a \cdot b \cdot u $$

$$ V_3 = u \cdot b \cdot u $$

Here too, volumes are proportional to their lengths:

$$ V_2 : V_3 = a : u $$

So:

$$ V_2 = \frac{a}{u} \cdot V_3 = a \cdot V_3 $$

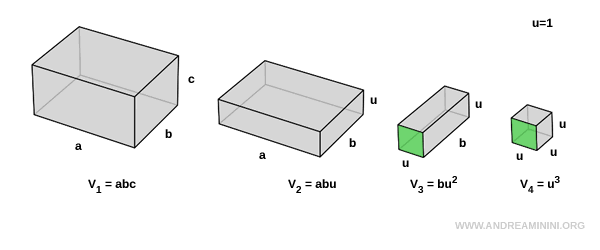
Next, consider the third and fourth prisms. They have the same face area $ u \cdot u $, but differ in width ( $ b $ vs $ u $ ):

$$ V_3 = u \cdot b \cdot u $$

$$ V_4 = u \cdot u \cdot u $$

Again, their volumes are in proportion:

$$ V_3 : V_4 = b : u $$

Therefore:

$$ V_3 = \frac{b}{u} \cdot V_4 = b \cdot V_4 $$

Returning to the first prism, we can now express its volume in terms of the others:

$$ V_1 = c \cdot V_2 $$

Since $ V_2 = a \cdot V_3 $, it follows that:

$$ V_1 = c \cdot (a \cdot V_3) $$

And since $ V_3 = b \cdot V_4 $, we get:

$$ V_1 = c \cdot (a \cdot (b \cdot V_4)) $$

This shows that the first prism contains $ a \cdot b \cdot c $ unit cubes of volume $ V_4 $:

$$ V_1 = a \cdot b \cdot c \cdot V_4 $$

Since $ V_4 = u^3 = 1 $, the final expression simplifies to:

$$ V_1 = a \cdot b \cdot c $$

This confirms that the volume of a rectangular prism is indeed the product of its length, width, and height.

And so on.