Right Prism

A right prism is a geometric solid with two parallel, congruent bases and rectangular lateral faces.

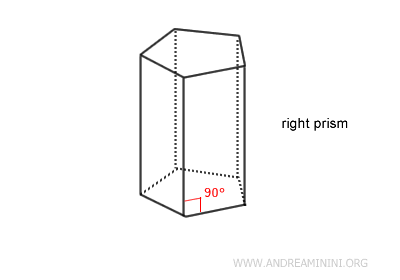
The bases can be any shape, but they are usually polygons (like triangles, squares, pentagons, etc.). They are identical in shape and size and are parallel to each other.

The lateral faces are all rectangles, with the number of lateral faces matching the number of sides of the base shape.

A right prism is a specific type of prism where the lateral faces are perpendicular to the bases. This means that the angles between the bases and the lateral faces are all right angles (90 degrees). Thanks to its simple and regular structure, it has many practical applications, especially in architecture and design.

The height of the prism is the perpendicular distance between the two bases.

Formulas for a Right Prism

Here are the key formulas for a right prism:

• Lateral Area
  The lateral surface area of a right prism can be calculated by multiplying the perimeter of the base (P) by the height (h) of the prism: $$ A_L = P \cdot h $$
• Total Surface Area
  The total surface area of the prism is the sum of the lateral area (A_L) and twice the area of the base (2A_B). In other words, it’s the sum of the areas of all the faces, including the bases. $$ A = A_L + 2A_B $$
• Volume
  The volume of a right prism is found by multiplying the area of one of the bases (A_B) by the height (h) of the prism: $$ V = A_B \cdot h $$

A Practical Example

Let’s consider a right prism with a pentagonal base, where each side of the pentagon is 3 cm long, and the height of the prism is 10 cm.

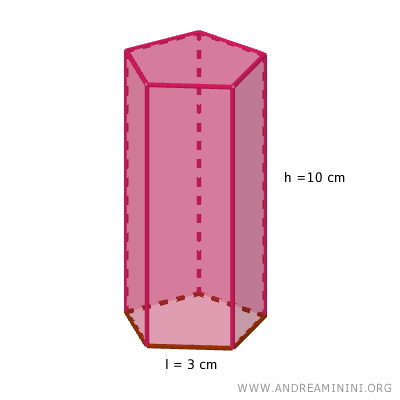
We need to calculate the total surface area and the volume of the prism.

First, let’s calculate the perimeter of the base (P_B) and the area of the base (A_B). Since both bases are congruent, we can use either one.

The base of this prism is a pentagon with each side measuring 3 cm.

Therefore, the perimeter of the base (P_B) is the sum of all five sides of the polygon, which gives us 15 cm.

$$ P_B = 3 \cdot 5 = 15 \ cm $$

To find the area of the pentagon, we calculate the apothem of the pentagon, using the side length of 3 cm and the fixed number for regular pentagons, which is approximately 0.688.

$$ a = 3 \cdot 0.688 = 2.064 $$

With the apothem (approximately a=2.064), we multiply it by the semiperimeter of the pentagon (p=P_B/2), where P_B=15 cm, to find the area of the pentagon, which is also the base area of the prism (A_B).

$$ A_B = a \cdot \frac{P_B}{2} $$

$$ A_B = 2.064 \cdot \frac{15}{2} = 15.48 \ cm^2 $$

Now that we have these values, we can calculate the total surface area and the volume of the right prism.

The lateral area (A_L) of the prism is calculated by multiplying the perimeter of the base (P_B=15 cm) by the height (h=10 cm).

$$ A_L = P_B \cdot h $$

$$ A_L = 15 \ cm \cdot 10 \ cm = 150 \ cm^2 $$

The total surface area (A) of the prism is the sum of the lateral area (A_L) and twice the base area (2A_B), where A_B=15.48 cm².

$$ A = A_L + 2A_B $$

$$ A = 150 \ cm^2 + 2 \cdot 15.48 \ cm^2 $$

$$ A = 150 \ cm^2 + 30.96 \ cm^2 $$

So, the total surface area of the prism is approximately 180.96 cm²

$$ A = 180.96 \ cm^2 $$

Finally, the volume of the prism is found by multiplying the base area (A_B=15.48 cm²) by the height (h=10 cm).

$$ V = A_B \cdot h $$

$$ V = 15.48 \ cm^2 \cdot 10 \ cm $$

Therefore, the volume of the prism is approximately 154.8 cm³

$$ V = 154.8 \ cm^3 $$

And that’s how you do it.