Associated Angles α and 3π/2-α in Trigonometry

In trigonometry, the associated angles alpha (α) and 3π/2-α allow the application of these transformation formulas: $$ \sin( \frac{3 \pi }{2} - \alpha ) = - \cos(\alpha) $$ $$ \cos( \frac{3 \pi }{2} - \alpha ) = - \sin(\alpha) $$ $$ \tan( \frac{3 \pi }{2} - \alpha ) = \cot(\alpha) $$ $$ \cot( \frac{3 \pi }{2} - \alpha ) = \tan(\alpha) $$

The angles α and 3π/2-α are associated angles, meaning they share the same absolute values for the trigonometric functions sine, cosine, tangent, and cotangent.

Proof and Explanation

Let's take an angle α and the angle 3π/2-α on a unit circle.

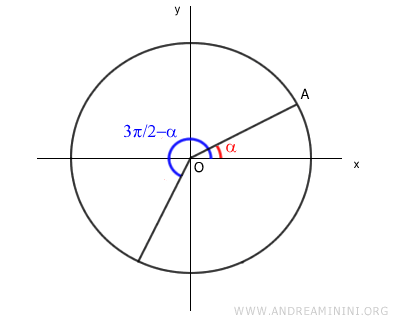
We construct two right triangles, OAB and OCD, within the unit circle.

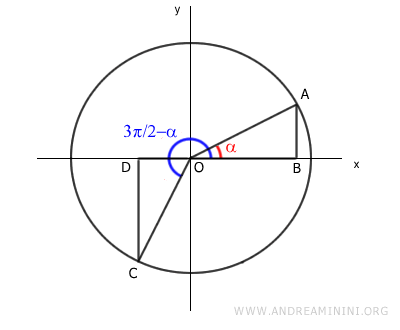
These right triangles, OAB and OCD, are congruent because they share the same acute angle (α) and the same hypotenuse.

This means that their corresponding sides have equal lengths.

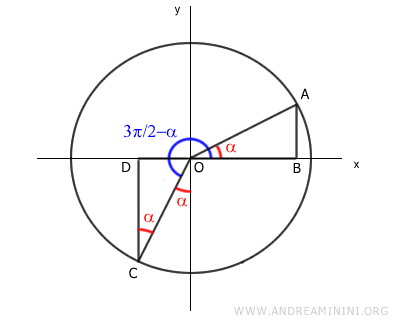
Note: Knowing that the sum of angles in a triangle is π (180°), triangle OCD has one angle of 90° (π/2) and another of (π/2-α) in the third quadrant. The remaining angle, obtained by subtraction, is α. $$ \pi = \frac{\pi}{2} + (\frac{\pi}{2} - \alpha ) + \alpha $$

The segment CD equals the segment OB.

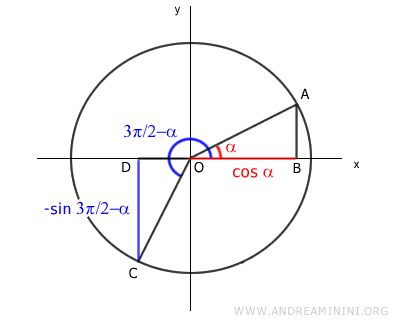
Here, segment CD represents the sine of 3π/2-α along the negative y-axis, while segment OB represents the cosine of α on the positive x-axis.

$$ - \sin \frac{3 \pi}{2} - \alpha = \cos \alpha $$

I multiply both sides of the equation by -1:

$$ (-1) \cdot ( - \sin \frac{3 \pi}{2} - \alpha ) = (-1) \cdot \cos \alpha $$

$$ \sin \frac{3 \pi}{2} - \alpha = - \cos \alpha $$

Therefore, the sine of 3π/2-α is equal to the negative cosine of α.

$$ \sin \frac{3 \pi}{2} - \alpha = - \cos \alpha $$

The segment AB is equal to the segment OD.

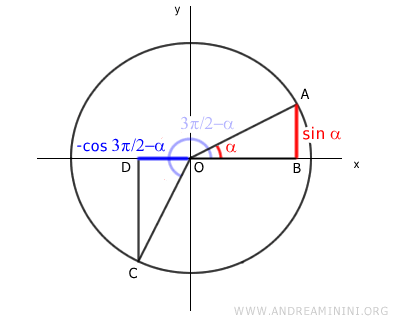
In this case, segment OD measures the cosine of 3π/2-α along the negative x-axis, while segment AB measures the sine of α along the positive y-axis.

$$ - \cos \frac{3 \pi}{2} - \alpha = \sin \alpha $$

Multiplying both sides by -1:

$$ (-1) \cdot ( - \cos \frac{3 \pi}{2} - \alpha ) = (-1) \cdot \sin \alpha $$

$$ \cos \frac{3 \pi}{2} - \alpha = - \sin \alpha $$

Thus, the cosine of 3π/2-α is equal to the negative sine of α.

$$ \cos \frac{3 \pi}{2} - \alpha = - \sin \alpha $$

Once the transformation formulas for sine and cosine are known, we can also derive the formulas for tangent and cotangent.

The tangent is the ratio between sine and cosine.

$$ \tan ( \frac{3 \pi}{2} - \alpha ) = \frac{ \sin (\frac{3 \pi}{2} - \alpha) }{ \cos ( 3 \frac{\pi}{2} - \alpha) } $$

Knowing that sin(3π/2-α) = - cos(α) and cos(3π/2-α) = - sin(α)

$$ \tan ( \frac{3 \pi}{2} - \alpha ) = \frac{ \sin (\frac{3 \pi}{2} - \alpha) }{ \cos ( 3 \frac{\pi}{2} - \alpha) } = \frac{ - \cos \alpha }{ - \sin \alpha } = \cot \alpha $$

Therefore, the tangent of the angle 3π/2-α is equal to the cotangent of α.

The cotangent is the ratio between cosine and sine.

$$ \cot ( \frac{3 \pi}{2} - \alpha ) = \frac{ \cos (\frac{3 \pi}{2} - \alpha) }{ \sin (\frac{3 \pi}{2} - \alpha) } $$

Given that sin(3π/2-α) = - cos(α) and cos(3π/2-α) = - sin(α)

$$ \cot ( \frac{3 \pi}{2} - \alpha ) = \frac{ \cos (\frac{3 \pi}{2} - \alpha) }{ \sin (\frac{3 \pi}{2} - \alpha) } = \frac{ - \sin \alpha }{ - \cos \alpha } = \tan \alpha $$

Therefore, the cotangent of the angle 3π/2-α is equal to the tangent of α.

A Practical Example

Let's calculate the sine of 210°

$$ \sin 210° $$

We rewrite the degrees as the difference of 270° - 60°

$$ \sin (270° - 60°) $$

Which, in radians, becomes:

$$ \sin (\frac{3 \pi}{2} - \frac{\pi}{3} ) $$

The angles 3π/2-α and α are associated angles where α=π/3 (i.e., 60°)

$$ \sin( \frac{3 \pi }{2} - \alpha ) = - \cos(\alpha) $$

$$ \sin( \frac{3 \pi }{2} - \frac{\pi}{3} ) = - \cos( \frac{\pi}{3} ) $$

Therefore, the sine of 210° is the negative of the cosine of 60°

Knowing that the cosine of 60° is 1/2, its negative value is -1/2.

$$ \sin( \frac{3 \pi }{2} - \frac{\pi}{3} ) = - \cos( \frac{\pi}{3} ) = - \frac{1}{2} $$

Thus, the sine of 210° is -1/2

$$ \sin 210° = - \frac{1}{2} $$

Simplifying the trigonometric function sin(210°) to the first quadrant as -1·cos(60°) made the calculation easier

And so on.