Associated Angles α and 2π-α in Trigonometry

In trigonometry, the angles alpha (α) and 2π-α are associated, allowing us to apply the following transformation formulas: $$ \sin(2 \pi - \alpha) = - \sin(\alpha) $$ $$ \cos(2 \pi - \alpha) = \cos(\alpha) $$ $$ \tan(2 \pi - \alpha) = - \tan(\alpha) $$ $$ \cot(2 \pi - \alpha) = - \cot(\alpha) $$

Because associated angles α and 2π-α are linked, their trigonometric functions—sine, cosine, tangent, and cotangent—share the same absolute values.

Proof and Explanation

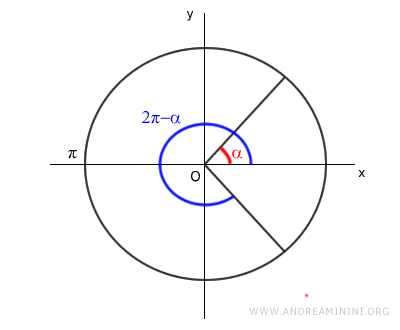
Let’s take the angle α and the angle 2π-α on the unit circle.

The angles α and π-α are supplementary angles because their sum equals 360° (2π), which is a full circle.

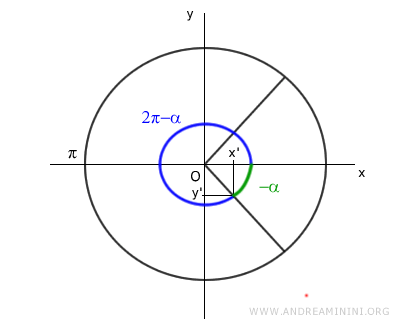
The sine (y') and cosine (x') values for the angle π-α (blue) are the same as those for the oriented angle -α (green).

This case can be proven using the same proof for opposite angles α and -α, which I recommend for further study.

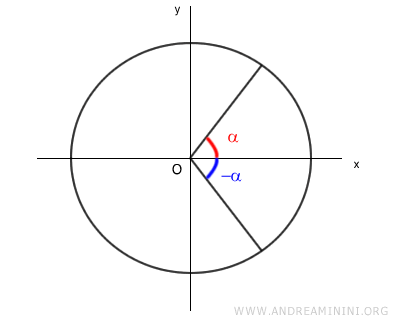
The transformation formulas for associated angles α and π-α, and those for α and -α, are identical.

A Practical Example

Let’s calculate the sine of 330°

$$ \sin 330° $$

We can rewrite this angle as 360° - 30°

$$ \sin 330° = \sin (360° - 30°) $$

In radians, this becomes

$$ \sin 330° = \sin \left( 2 \pi - \frac{\pi}{6} \right) $$

The angles 2π-α and α are associated, with α=π/6 (which corresponds to 30°).

$$ \sin( 2 \pi - \alpha ) = - \sin(\alpha) $$

Therefore, the sine of 330° is the negative of the sine of 30°

$$ \sin 330° = \sin \left( 2 \pi - \frac{\pi}{6} \right) = - \sin \left( \frac{\pi}{6} \right) $$

Since we know the sine of 30° is 1/2, the sine of 330° is -1/2.

$$ \sin 330° = \sin \left( 2 \pi - \frac{\pi}{6} \right) = - \sin \left( \frac{\pi}{6} \right) = - \frac{1}{2} $$

$$ \sin 330° = - \frac{1}{2} $$

And that's how it works.