Associated angles α and -α in trigonometry

In trigonometry, the associated angles alpha (α) and minus alpha (-α) allow us to apply the following transformation formulas: $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$

Since associated angles α and -α have the same absolute values for their trigonometric functions — sine, cosine, tangent, and cotangent — their relationships can be described by these formulas.

Explanation and proof

Let’s take an angle α and its opposite, -α, on the unit circle.

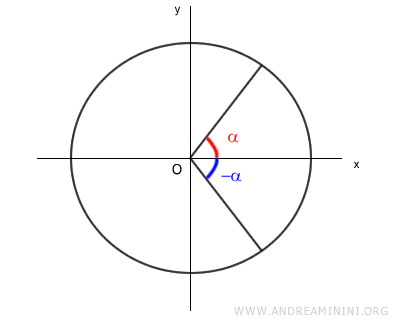
α and -α are known as opposite angles.

Next, we analyze the values of the trigonometric functions at these angles.

Sine

The opposite angles α and -α produce opposite values for the sine function on the y-axis: sin(α) and sin(-α).

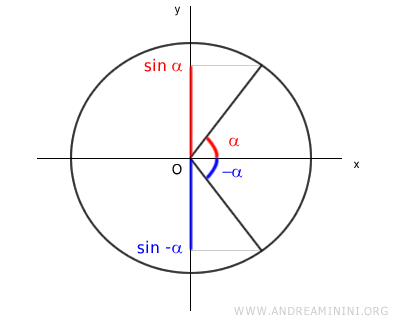
Since α and -α are associated angles, their sine values are equal in absolute terms.

$$ \sin \alpha = | \sin - \alpha |$$

Because the sine function is an odd function, f(-x)=-f(x), we can express sin(-α) as -sin(α).

$$ \sin - \alpha = - \sin \alpha $$

These two forms are equivalent.

Cosine

For opposite angles α and -α, the cosine function produces the same value on the x-axis: cos(α) and cos(-α).

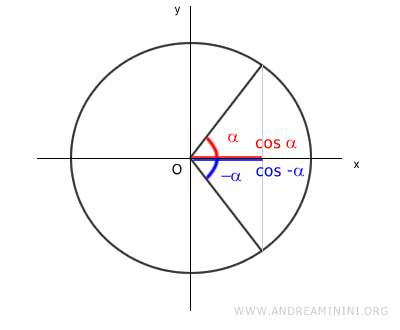
The cosine values are also equal in absolute terms.

$$ \cos \alpha = | \cos - \alpha |$$

Because the cosine function is an even function, f(-x)=f(x), we can write cos(-α) as cos(α).

$$ \cos - \alpha = \cos \alpha $$

These two forms are equivalent.

Once we understand the equivalence for sine and cosine of α and -α, we can easily determine the same for tangent and cotangent.

Tangent

The tangent of an angle is the ratio of sine to cosine.

$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$

For the angle -α, the tangent becomes:

$$ \tan -\alpha = \frac{\sin -\alpha}{\cos -\alpha} $$

Since sin(-α) = -sin(α) and cos(-α) = cos(α), we can write:

$$ \tan -\alpha = \frac{-\sin \alpha}{\cos \alpha} $$

Thus, the tangent of -α equals minus the tangent of α:

$$ \tan -\alpha = -\tan \alpha $$

Next, let’s demonstrate the equivalence for cotangent, the reciprocal of the tangent.

Cotangent

The cotangent of an angle is the ratio of cosine to sine.

$$ \cot \alpha = \frac{\cos \alpha}{\sin \alpha} $$

For the angle -α, the cotangent is:

$$ \cot -\alpha = \frac{\cos -\alpha}{\sin -\alpha} $$

Since sin(-α) = -sin(α) and cos(-α) = cos(α), we can write:

$$ \cot -\alpha = \frac{\cos \alpha}{ -\sin \alpha} $$

Therefore, the cotangent of -α is equal to minus the cotangent of α:

$$ \cot -\alpha = - \cot \alpha $$

At this point, all the transformation formulas for α and -α have been demonstrated.

A practical example

Let’s calculate the sine of -30°:

$$ \sin -30° $$

In radians, this is:

$$ \sin - 30° = \sin ( - \frac{\pi}{6} ) $$

Since the opposite angles α=π/6 and -α=-π/6 are associated angles:

$$ \sin( \alpha ) = - \sin(\alpha) $$

So, the sine of -30° is the opposite of the sine of 30°:

$$ \sin -30° = \sin ( - \frac{\pi}{6} )= - \sin( \frac{\pi}{6} ) $$

Knowing that the sine of 30° is 1/2, the sine of -30° is -1/2:

$$ \sin -30° = - \frac{1}{2} $$

And so on.