Even Functions

What is an even function?

A function is called even if, for every x in its domain, the following condition holds: $$ f(x) = f(-x) \ \ \ \forall \ x \ \in D $$

If a function is even, its graph is symmetric with respect to the y-axis, because for every point P(x, y), there is a corresponding point P(-x, y).

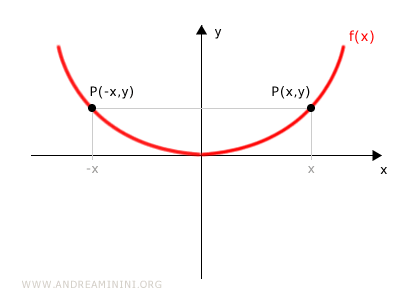
How can you check if a function is even?

• Analytically, you calculate f(-x) by substituting the variable x with its opposite, -x, and compare the result with f(x). If the two are equal, the function is even. $$ f(-x) = f(x) $$

  Example: Let's take the function f(x) = x². By substituting x with -x, we can check if we get the same function. $$ f(-x) = (-x)^2 = x^2 = f(x) $$ Since f(-x) equals f(x), the function is even.

• Graphically, you simply observe if the graph is symmetrical with respect to the y-axis.
  

  

Note: Just because a function isn't even doesn't mean it's odd. And vice versa. For instance, the function f(x) = x² + x is neither even nor odd.

A Practical Example

A classic example of an even function is the cosine function.

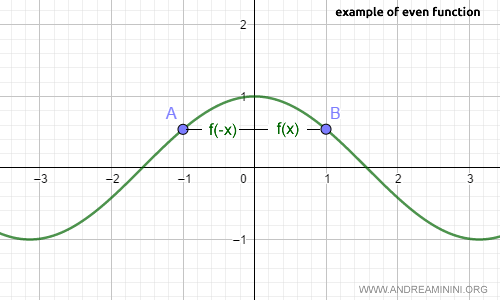
For every x in the cosine's domain, the relation f(x) = f(-x) holds, and its graph is symmetric about the y-axis.

Note: For example, at x = 1 and x = -1, the cosine function gives the same value, i.e., f(1) = f(-1), and so on.

Example 2

Another example of an even function is f(x) = x².

$$ f(x) = x^2 $$ $$ f(-x) = (-x)^2 = x^2 $$

Here too, for every value in the domain, f(x) equals f(-x).

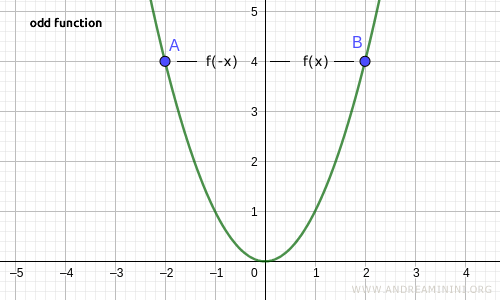
Note: In general, if a function contains only even powers of x, it is an even function.

Example 3

Let’s verify analytically if the following function is even:

$$ f(x) = x^2 + x $$

Substitute x with -x in the function:

$$ f(-x) = (-x)^2 + (-x) = x^2 - x $$

The result is different from f(x) = x² + x.

Thus, this is not an even function.

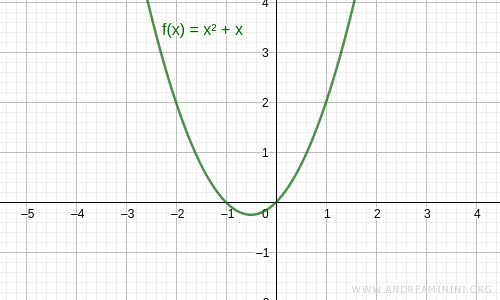
Note: The function f(x) = x² + x is also not an odd function.

And so on.