Functions of Two Variables
What Is a Function of Two Variables?
A function of two variables assigns a unique value z (codomain) to each pair of values (x, y) in its domain. $$ z=f(x,y) $$
In real functions, the domain (or definition set) consists of pairs of real numbers.
$$ R^2 = [(x,y) : x,y \in R] $$
The codomain, on the other hand, is a set of real numbers.
$$ f: \: R^2 \rightarrow R $$
Note: Here, x and y are the independent variables, while z is the dependent variable. However, the choice of variable names is arbitrary. $$ f: \: (x,y) \rightarrow z $$
How to Represent a Function of Two Variables
Representation in Three-Dimensional Space
To graphically represent a function of two variables, we use a Cartesian coordinate system with three axes: x, y, and z.
This creates a diagram in three-dimensional space.
The (x, y) plane is the Cartesian product of the real numbers, denoted as R2 or RxR.
Therefore, the domain of a function with two variables is a subset of the (x, y) plane.
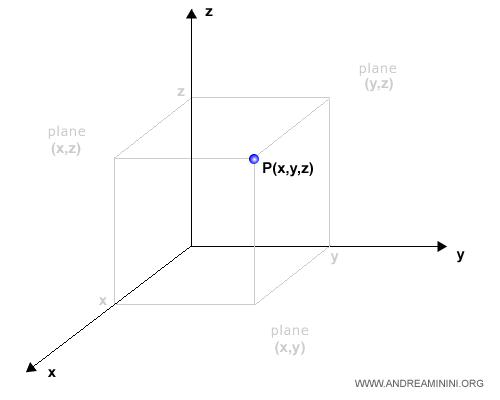
Each pair (x, y) in the domain corresponds to a value on the z-axis, where z = f(x, y).
Thus, the codomain of a function with two variables is represented as a point in three-dimensional space.
Note: Each value of a function with two variables corresponds to a point in three-dimensional space with coordinates (x, y, z).
Representation on a Plane
You can also represent a function z=f(x,y) on a two-dimensional plane by relating the variables in pairs, such as (x, z) and (y, z).
In this case, two separate graphs are required.
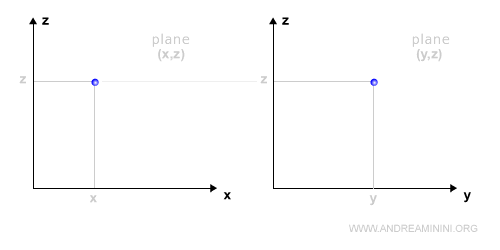
This approach is useful for highlighting the relationships between each independent variable and the dependent variable.
Note: The independent variable not shown is projected onto the plane of the remaining variables through orthogonal projection.
How to Plot the Graph of a Function of Two Variables
The most effective way to plot a function of two variables is the point-by-point method, which is also how computers generate such graphs.
- Start by laying out a grid of points in the Oxy plane, representing the independent variables of the function f(x,y).
- Calculate the value of z = f(x,y) at each grid point.
- Connect neighboring points with lines to form a mesh.
The result is a three-dimensional surface plotted in space.
Example
Consider the function:
$$ z= f(x,y) = \frac{3}{x+y+1} $$
First, I create a grid of points in the Oxy plane for the independent variables.
For example, let’s look at the portion of the plane bounded by the points (0,0) and (3,3).
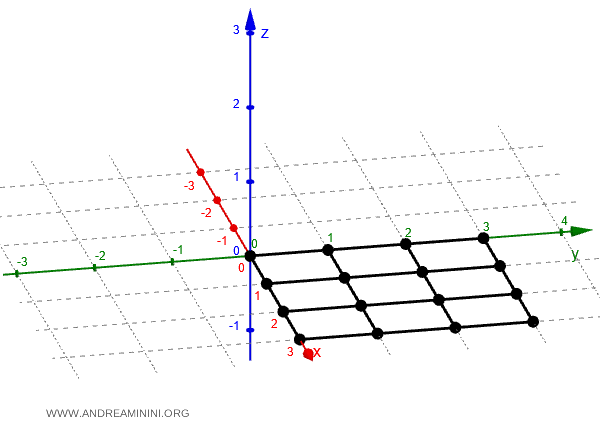
Next, I compute the value of $ z $ at each point.
| x | y | z = 3 / (x + y + 1) |
|---|---|---|
| 0 | 0 | 3.0 |
| 0 | 1 | 1.5 |
| 0 | 2 | 1.0 |
| 0 | 3 | 0.75 |
| 1 | 0 | 1.5 |
| 1 | 1 | 1.0 |
| 1 | 2 | 0.75 |
| 1 | 3 | 0.6 |
| 2 | 0 | 1.0 |
| 2 | 1 | 0.75 |
| 2 | 2 | 0.6 |
| 2 | 3 | 0.5 |
| 3 | 0 | 0.75 |
| 3 | 1 | 0.6 |
| 3 | 2 | 0.5 |
| 3 | 3 | 0.4 |
For each point (x, y), I then draw a vertical line parallel to the $ z $-axis, with a height equal to the computed value. Finally, I join adjacent points to form a continuous surface.

This process produces the surface that represents the function $ f(x,y) $.
A Practical Example
Here's an example of a function with two variables:
$$ z= f(x,y) = x^2-y^2 $$
The graphical representation of this function in three-dimensional Cartesian coordinates is shown below:
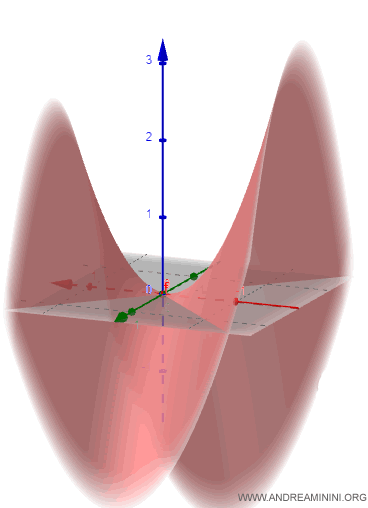
This surface is known as a hyperbolic paraboloid.
To represent the function on a plane, first set the x variable to zero:
$$ z= f(0,y) = -y^2 $$
Then set the y variable to zero:
$$ z= f(x,0) = x^2 $$
By doing this, you obtain the projections of the function on the (y, z) and (x, y) planes.
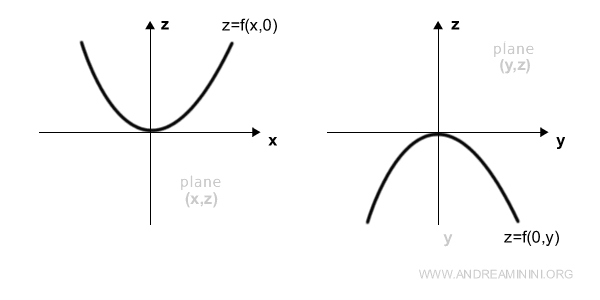
And so on.
