Circular Neighborhood

In the vector space $\mathbb{R^2} = \mathbb{R} \times \mathbb{R}$, a circular neighborhood (or open disk) is an open circle centered at the point $(x_0, y_0)$ with a positive radius $\delta > 0$. $$ I_{\delta} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta \} $$

The set $I_{\delta}$ is a subset of the space $\mathbb{R^2}$.

This is called an "open" neighborhood because it excludes the points that lie on the circumference of the circle with radius $\delta$ centered at $(x_0, y_0)$, including only the points within it.

All points $(x, y)$ that satisfy the condition $\sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta$ are part of the circular neighborhood $I_{\delta}$, known as "interior points" of $I_{\delta}$, and they constitute what is called the "interior" of $I_{\delta}$. For example, point A.

Conversely, points that do not belong to the circular neighborhood $I_{\delta}$ are outside the open circle and are referred to as "exterior points" of $I_{\delta}$. For example, point B.

These points are part of the complement of the neighborhood, denoted as $\overline{I}_{\delta} = \mathbb{R^2} - I_{\delta}$.

Points $(x, y)$ that lie exactly on the circumference with radius $\delta$, that is, those for which $\sqrt{(x - x_0)^2 + (y - y_0)^2} = \delta$, are called "boundary points". These points are not part of the open neighborhood $I_{\delta}$ and form the boundary of the neighborhood. For example, point C.

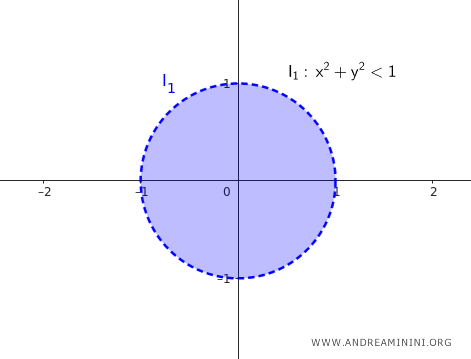
Note. If the circular neighborhood is "open," it does not include the boundary points. For instance, the open circular neighborhood centered at (0,0) with radius $ \delta = 1 $ is $$ I_{1 \ open} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} $$ In this case, the neighborhood includes all points whose distance from the center (0,0) is less than $ \delta = 1 $

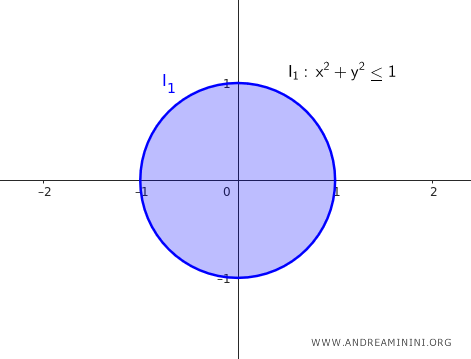
If the circular neighborhood is "closed," it includes the boundary points as well $$ I_{1 \ closed} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} \le 1 \} $$ In this case, the distance condition is "less than or equal to" the radius $ \delta = 1 $, so it includes the points on the circumference, or the "edge" of the circle.

In general, in the standard topology on $ \mathbb{R^2} $, neighborhoods are always considered open sets, meaning they do not include boundary points. Closed sets, on the other hand, are the complement of open sets, denoted as $ C = \mathbb{R^2} - A $. Therefore, there can also be sets that are both open and closed, known as "clopen" sets. For example, the empty set $ \emptyset $ and the entire set $ \mathbb{R^2} $ are considered "open" in any topology. Since one is the complement of the other ( $ \mathbb{R^2} - \emptyset = \mathbb{R^2} $ and $ \mathbb{R^2} - \mathbb{R^2} = \emptyset $ ), they are also "closed". Thus, the sets $ \emptyset $ and $ \mathbb{R^2} $ are both open and closed. However, these concepts can be challenging for those new to topology, for which I recommend further study.

All points $ (x,y) $ that, for any radius $ \delta $, have a circular neighborhood containing at least one other point of $ I_{\delta} $ different from $(x, y)$ are called "accumulation points" of $ I_{\delta} $.

Therefore, all interior points and boundary points of $ I_{\delta} $ are accumulation points of $ I_{\delta} $.

For instance, point A and point C are accumulation points of $ I_{\delta} $, while exterior point B is not.

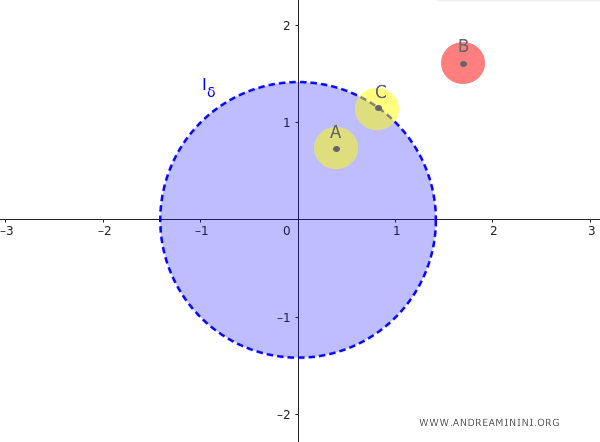
It is important to note that an accumulation point may not necessarily belong to the set itself. For example, boundary point C is not an element of the open set $ I_{\delta} $ but is still an accumulation point of $ I_{\delta} $.

Moreover, for a point $(x;y)$ to be an accumulation point, every neighborhood around it, with any radius $ \delta >0 $, must contain at least one point of $ I_{\delta} $ different from $(x;y).

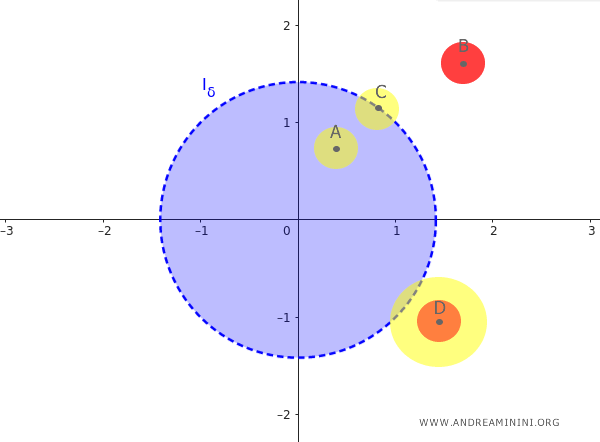
For example, exterior point D has a sufficiently large circular neighborhood (yellow) that includes a point from $ I_{\delta} $, but this is not true for every possible radius $ \delta >0$. There are also neighborhoods of D with smaller radii (red) that do not contain points from $ I_{\delta} $, so point D is not an accumulation point.

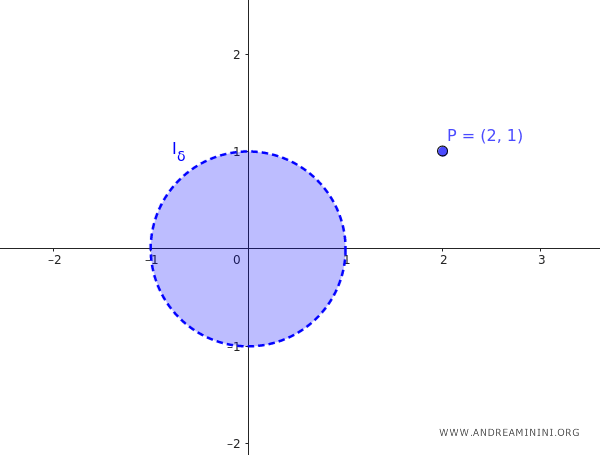
Note. If a point in $ I_{\delta} $ is not an accumulation point, it is called an "isolated point" of $ I_{\delta} $. For example, a set $ A $ consists of a circular neighborhood centered at (0,0) with radius $ \delta = 1 $ and the point P(2;1). $$ A = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} \cup \{ P(2;1) \} $$ Point P(2;1) is an isolated point of set A because it belongs to set A but is not an accumulation point of A.

The union of the points in the circular neighborhood $ I_{\delta} $ with the accumulation points of $ I_{\delta} $ is called the "closure" of the set $ I_{\delta} $. It is denoted by $ \overline{I}_{\delta} $ or $ \text{Cl}(I_{\delta}) $.

In other words, the closure of $ I_{\delta} $ is the set that includes the points in the neighborhood $ I_{\delta} $ along with its boundary points.

The closure of $ I_{\delta} $ is a closed set.

Note. The closure of $ I_{\delta} $ can also be seen as the intersection of all closed sets that contain $ I_{\delta} $.

If a neighborhood A is an open set, its closure in the space $ \mathbb{R^2} $ is also known as the domain of $ \mathbb{R^2} $.

And so on.