Limits of Functions of Two or More Variables

Consider a function of two variables, f(x, y): $$ f:\mathbb{R}^2 \rightarrow \mathbb{R} $$ The limit of the function is $$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) $$ which can also be expressed by treating the pair (x, y) as a vector in two dimensions: $$ \lim_{\vec{x} \rightarrow \vec{x}_0} f( \vec{x} ) $$ where $$ \vec{x} = (x,y) \\ \vec{x}_0 = (x_0,y_0) $$

When dealing with the limit of a function of two variables like f(x, y), the concept is similar to that of single-variable limits - but with added complexity due to the multidimensional domain.

Why limits matter

A limit describes how the function f(x, y) behaves as the point (x₀, y₀) is approached.

There are several possible scenarios:

• The function converges to a real number
  The limit is a finite real number, representing a specific height on the z-axis.
• The function diverges to positive or negative infinity
  The limit exists in the extended sense, but its value grows without bound. For instance, if the limit is +∞, the values of f(x, y) increase arbitrarily as (x, y) approaches (x₀, y₀).
• The limit does not exist
  The function neither converges nor diverges at that point; the behavior is too erratic or inconsistent to define a limit.

Note. The concept of a limit is the same as for functions of a single variable, f(x). However, with two independent variables (x, y), each point represents a location in the plane, not just on a line. The neighborhood around the point (x₀, y₀) is now a circular region - a disk of radius δ - rather than an interval on the real line.

The limit of a function of two variables at a point \((x_0, y_0)\) exists only if the function approaches the same value along every possible path leading to that point.

This includes both straight-line paths, such as \(y = mx\), and curved ones, like \(y = x^2\) or \(x = \rho \cos\theta,\, y = \rho \sin\theta\).

Therefore, if I can identify even two paths approaching \((x_0, y_0)\) that yield different limits, I can definitively conclude that the limit does not exist at that point.

Convergent Limit to a Real Number l

The limit of a function of two variables \(f(x,y)\) is said to equal a finite real number \(l\) if, as \((x,y)\) approaches \((x_0, y_0)\), the function values approach \(l\): $$ \lim_{(x, y) \to (x_0, y_0)} f(x, y) = l $$ More formally, for every \(\epsilon > 0\), there exists a radius \(\delta > 0\) such that, for all points \((x,y)\) within that radius - excluding the center - we have \(|f(x,y) - l| < \epsilon\).

The limit of the function f(x, y) as it approaches the point (x₀, y₀) exists and is finite if:

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = l \ \in \ \mathbb{R} $$

That is, for every positive number ε (no matter how small), there exists a corresponding δ > 0 such that for all points (x, y) within a distance δ of (x₀, y₀), but not equal to it, the function value f(x, y) stays within ε units of l:

$$ \forall \varepsilon > 0 \ \exists \ \delta > 0 \ : \ \forall \ (x,y) \in B_\delta(x_0,y_0) - \{ (x_0,y_0) \} \ , \ l - \varepsilon < f(x,y) < l + \varepsilon $$

Here, \(B_\delta(x_0, y_0)\) is the open disk of radius \(\delta\), centered at \((x_0, y_0)\).

An equivalent way to write this is using the absolute value notation:

\[ \forall \varepsilon > 0\ \exists \ \delta > 0 \ :\ \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\} \ , \ |f(x, y) - l| < \varepsilon \]

From a graphical perspective, this means that within every circular neighborhood of radius \(\delta\) around the point \((x_0, y_0)\), the surface defined by \(f(x, y)\) lies between \(l - \varepsilon\) and \(l + \varepsilon\).

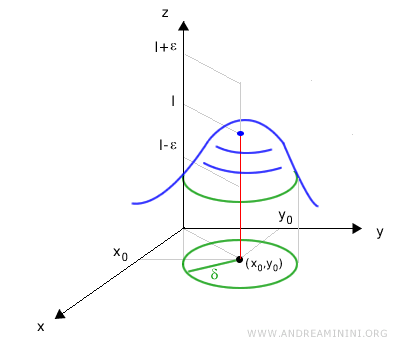
In other words, as (x, y) gets closer to (x₀, y₀), the graph of the function increasingly flattens out near the plane \(z = l\).

Divergence to Positive Infinity

A function of two variables \(f(x,y)\) is said to diverge to \(+\infty\) as \((x, y)\) approaches a point \((x_0, y_0)\) if the values of \(f(x, y)\) grow without bound. Formally, this means that for every real number \(M > 0\), there exists a radius \(\delta > 0\) such that for all points \((x, y)\) within that distance from \((x_0, y_0)\), but not equal to it, we have \(f(x, y) > M\).

In symbols, the function diverges to positive infinity at the point \((x_0, y_0)\) if

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = + \infty $$

That is, for any real number \(M\), there exists an open neighborhood \(B_\delta(x_0, y_0)\) such that the function exceeds \(M\) at every point in the neighborhood except the center:

$$ \forall M > 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) > M $$

Geometrically, this neighborhood is an open disk in the \(xy\)-plane centered at \((x_0, y_0)\), while \(M\) represents a height along the \(z\)-axis.

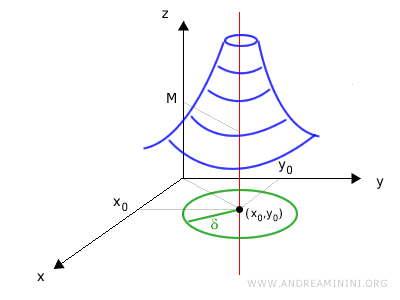
In essence, saying \(f(x, y) > M\) means the graph of the function rises indefinitely above any chosen level as \((x, y)\) gets closer to \((x_0, y_0)\).

Divergence to Negative Infinity

A function of two variables \(f(x,y)\) diverges to \(-\infty\) at a point \((x_0, y_0)\) if the values of \(f(x,y)\) decrease without bound as \((x,y)\) approaches \((x_0, y_0)\). Formally, this means that for every real number \(M < 0\), there exists a radius \(\delta > 0\) such that for all points \((x,y)\) within that distance of \((x_0, y_0)\), but not equal to it, we have \(f(x,y) < M\).

The limit of the function at that point is:

$$ \lim_{(x,y)\rightarrow(x_0,y_0)} f(x,y) = - \infty $$

That is, for any negative real number \(M\), there exists an open disk centered at \((x_0, y_0)\) of radius \(\delta\) such that \(f(x, y) < M\) for all points in the disk, except the center:

$$ \forall M < 0\ \exists \delta > 0 : \forall (x, y) \in B_\delta(x_0, y_0) \setminus \{(x_0, y_0)\},\ f(x, y) < M $$

Graphically, this means that within any such neighborhood \(B_\delta(x_0, y_0)\), the surface defined by \(f(x, y)\) dips below any horizontal level \(z = M\), no matter how low.

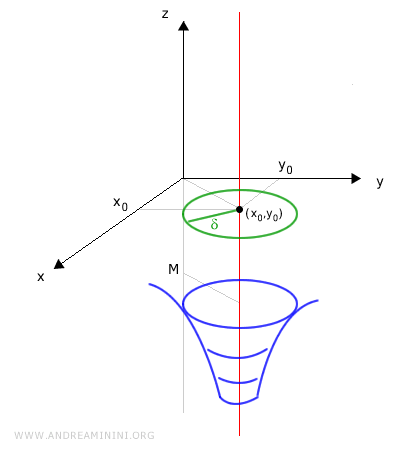
In other words, the surface represented by \(z = f(x, y)\) falls away indefinitely as \((x, y)\) approaches \((x_0, y_0)\).

A Practical Example

Let’s evaluate the limit of the function \(f(x, y)\) as the point \((x, y)\) approaches the origin:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} $$

This is an indeterminate form of type 0/0:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = \frac{0}{0} $$

To evaluate the limit, we’ll use the Squeeze Theorem.

First, notice that the function is non-negative for all values of (x, y), since all powers involved are even:

$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} $$

We can also show that the function is bounded above by \(y^4\):

$$ 0 \le \frac{x^2 \cdot y^4}{x^2 + y^2} \le y^4 $$

Explanation. We can rewrite the expression as: $$ \frac{x^2 \cdot y^4}{x^2 + y^2} = y^4 \cdot \frac{x^2}{x^2 + y^2} $$ The second factor, \( \frac{x^2}{x^2 + y^2} \), is always between 0 and 1 because the denominator is always greater than or equal to the numerator. So we’re multiplying \(y^4\) by a factor \(k\) such that \(0 \le k \le 1\). This gives us: $$ y^4 \cdot \frac{x^2}{x^2 + y^2} \le y^4 $$

Now we apply the limit to each part of the inequality:

$$ \lim_{(x,y) \rightarrow (0,0)} 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le \lim_{(x,y) \rightarrow (0,0)} y^4 $$

Both the left-hand and right-hand limits tend to 0 as \((x, y) \to (0, 0)\):

$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} \le 0 $$

Therefore, by the Squeeze Theorem, the middle limit must also be 0:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2 \cdot y^4}{x^2 + y^2} = 0 $$

And that completes the proof.