Directional Derivative

The directional derivative of a function \( f \) at a point \( (x_0, y_0) \) in the direction of the vector \( \vec{v} = (\alpha, \beta) \) is defined as \[ \frac{\partial f}{\partial \vec{v}}(x_0,y_0) = \lim_{t \to 0} \frac{f(x_0 + t\alpha, \; y_0 + t\beta) - f(x_0, y_0)}{t} \]

In essence, we take a small step \( t \) in the direction of \( \vec{v} \), observe how much the function \( f \) changes, and divide by the length of the step.

This limit exists if and only if the result is a real, finite number.

The directional derivative generalizes the concept of the partial derivative, which measures change along a coordinate axis.

In fact, if we choose \( \vec{v} = (1,0) \) or \( (0,1) \) - that is, in the direction of the x- or y-axis - the directional derivative reduces to the corresponding partial derivative.

Note. A function of two variables defines a surface in three-dimensional space. For instance, if the graph resembles a “hill” and the point \( (x_0, y_0) \) lies on its slope, then the directional derivative tells us how steeply the surface rises or falls in the direction of the vector \( \vec{v} \). This direction isn’t limited to the x or y axis - it can point diagonally, or in any direction at all.

Geometrically, the directional derivative measures the rate of change of the function along the line defined by the parametric equation \( (x_0 + t\alpha, y_0 + t\beta) \).

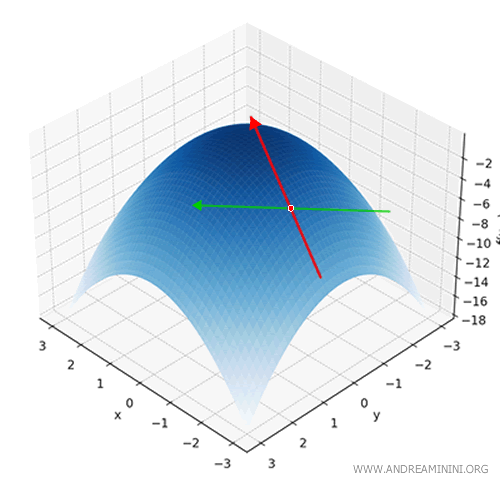
In other words, we move along a line starting at \( (x_0, y_0) \) and heading in the direction of \( \vec{v} = (\alpha, \beta) \):

\[ (x(t), y(t)) = (x_0 + t\alpha, \; y_0 + t\beta) \]

The directional derivative tells us how rapidly the function \( f \) increases or decreases as we move in that direction.

To put it plainly: it’s the slope of the surface if you were climbing in that direction - or sliding down, if you’re heading the other way.

Note. More generally, for a function \( f: \mathbb{R}^n \to \mathbb{R} \), where \( \vec{x}_0 \in \mathbb{R}^n \) represents a point in space and \( \vec{v} \in \mathbb{R}^n \) is a non-zero direction vector, the directional derivative of \( f \) at \( \vec{x}_0 \) in the direction of \( \vec{v} \) is defined in vector notation as: \[ \frac{\partial f}{\partial \vec{v}}( \vec{x}_0 ) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t \vec{v}) - f(\vec{x}_0)}{t} \] Here, \( \vec{x}_0 \) is a vector with coordinates \( (x_1, x_2, ..., x_n) \), representing a point in \( \mathbb{R}^n \).

A Concrete Example

Let’s consider the function

\[ f(x, y) = x^2 + y^2 \]

This function defines a paraboloid - a bowl-shaped surface - and is easy to differentiate.

We’ll examine how the function \( f(x, y) = x^2 + y^2 \) changes as we move from the point \( (1, 2) \) in the direction of the vector \( \vec{v} = (3, 4) \).

First, we normalize the direction vector.

To compute the directional derivative correctly, the direction vector must be a unit vector - that is, it must have length 1.

The magnitude of \( \vec{v} = (3, 4) \) is:

\[ \|\vec{v}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

So, the unit vector is:

\[ \hat{v} = \left(\frac{3}{5}, \frac{4}{5} \right) \]

Next, we compute the gradient \( \nabla f(x, y) \), which consists of the partial derivatives:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (2x, 2y) \]

Evaluating at the point \( (1, 2) \):

\[ \nabla f(1, 2) = (2 \cdot 1, 2 \cdot 2) = (2, 4) \]

We now take the dot product of the gradient and the unit vector \( \hat{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(1, 2) = \nabla f(1, 2) \cdot \hat{v} = (2, 4) \cdot \left( \frac{3}{5}, \frac{4}{5} \right) \]

\[ = \frac{2 \cdot 3 + 4 \cdot 4}{5} = \frac{6 + 16}{5} = \frac{22}{5} \]

So, the directional derivative of \( f(x,y) = x^2 + y^2 \) at the point \( (1,2) \) in the direction \( \vec{v} = (3,4) \) is:

\[ \frac{\partial f}{\partial \vec{v}}(1,2) = \frac{22}{5} \]

This tells us that, at the point \( (1,2) \), if we move in the direction \( (3,4) \), the function increases at a rate of \( \frac{22}{5} \).

The Directional Derivative Theorem

If the function \( f \) is differentiable at a point \( \vec{x}_0 \), then its directional derivative at \( \vec{x}_0 \) in the direction of a vector \( \vec{v} \) is given by the dot product of the gradient of \( f \) at that point and the direction vector \( \vec{v} \): \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] This is often written as \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \] Here, the gradient \( \vec{\alpha} = \nabla f(x_0) \) points in the direction of the steepest ascent of the function.

The dot product with \( \vec{v} \) quantifies how much of the function’s rate of change is aligned with the direction \( \vec{v} \).

If \( \vec{v} \) is orthogonal to the gradient, the directional derivative is zero.

If \( \vec{v} \) is aligned with the gradient, the directional derivative attains its maximum value in that direction.

Example

Let’s consider the function

\[ f(x,y) = x^2 + y^2 \]

We’ll examine the point \( \vec x_0 = (1,\,2) \) and the direction vector \( \vec v = (3,\,4) \).

First, we compute the gradient of \(f(x,y)\):

\[ \nabla f(x,y) = \bigl(\,\partial_x f,\;\partial_y f\bigr) = (2x,\;2y). \]

Evaluating the gradient at the point \(\vec x_0 = (1,2)\) gives:

\[ \nabla f(1,2) = (2\cdot1,\;2\cdot2) = (2,\;4) \]

The (non-unit) directional derivative of \(f\) in the direction of \(\vec v\) is given by:

\[ \frac{\partial f}{\partial \vec v}(\vec x_0) = \nabla f(\vec x_0)\;\cdot\;\vec v \]

We now compute the dot product between \(\nabla f(1,2)\) and \(\vec v\):

\[ \frac{\partial f}{\partial \vec v}(1,2) = \nabla f(1,2)\cdot (3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = (2,4)\cdot(3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 2\cdot3 + 4\cdot4 = 6 + 16 \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 22 \]

This result, 22, represents the rate of change of \(f\) in the (non-normalized) direction of \((3,4)\).

To compute the unit directional derivative, we normalize the direction vector:

\[ \|\vec v\| = \sqrt{3^2 + 4^2} = 5, \qquad \hat v = \left(\tfrac{3}{5},\,\tfrac{4}{5}\right) \]

Then, the directional derivative in the direction of the unit vector \(\hat v\) becomes:

\[ D_{\hat v}f(1,2) = \nabla f(1,2)\cdot \hat v = (2,4)\cdot\left(\tfrac{3}{5},\tfrac{4}{5}\right) = \frac{1}{5}(2\cdot3 + 4\cdot4) \]

\[ = \frac{22}{5} = 4.4 \]

So 4.4 is the rate of change of the function per unit length in that direction.

This example clearly illustrates how the gradient yields the directional derivative directly through the dot product with a given direction vector.

To visualize the function in three dimensions, the surface defined by \( f(x, y) = x^2 + y^2 \) takes the shape of a paraboloid - resembling an upward-facing bowl or an inverted dome.

The red point \( \vec{x}_0 = (1, 2) \) indicates the specific point under analysis.

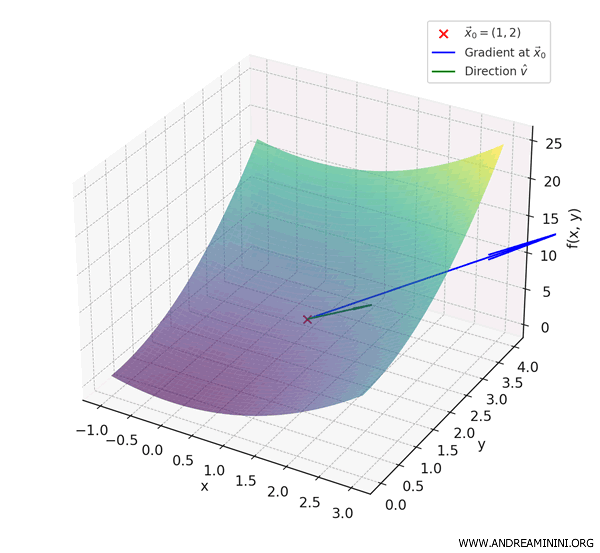
The blue vector represents the gradient at \( \vec{x}_0 \); it points in the direction of the steepest increase of the function.

The green vector corresponds to the unit direction \( \hat{v} \), showing the rate at which the function increases when moving in that specific direction.

Proof

We aim to prove that if \( f \) is differentiable at \( \vec{x}_0 \), then the directional derivative of \( f \) at \( \vec{x}_0 \) in the direction of \( \vec{v} \) equals the dot product of the gradient \( \vec{\alpha} \) (i.e., the linear approximation of \( f \) at \( \vec{x}_0 \)) and the vector \( \vec{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Assume \( f \) is differentiable at \( \vec{x}_0 \). By definition, this means:

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(|\vec{h}|) \quad \text{as } \vec{h} \to 0 \]

This is the first-order Taylor approximation, where \( \vec{\alpha} \) represents the gradient of \( f \) at \( \vec{x}_0 \), and \( o(|\vec{h}|) \) denotes a higher-order infinitesimal - i.e., a term that becomes negligible compared to \( |\vec{h}| \) as \( \vec{h} \to 0 \).

Now, take an arbitrary unit vector \( \vec{v} \) indicating a direction. The directional derivative of \( f \) at \( \vec{x}_0 \) along \( \vec{v} \) is defined by the following limit:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) := \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

To evaluate this, apply the differentiability expansion with \( \vec{h} = t\vec{v} \):

\[ f(\vec{x}_0 + t\vec{v}) = f(\vec{x}_0) + \vec{\alpha} \cdot (t\vec{v}) + o(|t\vec{v}|) \]

Substituting into the definition of the directional derivative yields:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

\[ = \lim_{t \to 0} \frac{f(\vec{x}_0) + t (\vec{\alpha} \cdot \vec{v}) + o(t|\vec{v}|) - f(\vec{x}_0)}{t} \]

The constant terms cancel, leaving:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \lim_{t \to 0} \frac{t (\vec{\alpha} \cdot \vec{v}) + o(t|\vec{v}|)}{t} \]

We now factor the numerator and split the limit:

\[ = \lim_{t \to 0} \left[ \vec{\alpha} \cdot \vec{v} + \frac{o(t|\vec{v}|)}{t} \right] \]

By the definition of the little-o notation, \( \frac{o(t|\vec{v}|)}{t|\vec{v}|} \to 0 \) as \( t \to 0 \), so the second term vanishes in the limit:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Thus, we have shown that the directional derivative is given by the dot product of the gradient of \( f \) at \( \vec{x}_0 \) and the direction vector \( \vec{v} \).

More Examples

Let’s consider the function of two variables \( f(x, y) = x^2 - xy \), and compute its directional derivative at the point \( (-1, 2) \) in the direction of the vector \( \mathbf{v} = (-1, 3) \).

We begin by computing the gradient \( \nabla f(x, y) \), which is the vector of partial derivatives:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]

The partial derivatives of the function are:

• \( \frac{\partial f}{\partial x} = 2x - y \)
• \( \frac{\partial f}{\partial y} = -x \)

So, the gradient vector is:

\[ \nabla f(x, y) = (2x - y, -x) \]

Next, we evaluate the gradient at the point \( (-1, 2) \) by substituting \( x = -1 \) and \( y = 2 \):

\[ \nabla f(-1, 2) = (2(-1) - 2, -(-1)) = (-2 - 2, 1) = (-4, 1) \]

To find the directional derivative, we take the dot product of the gradient vector \( (-4, 1) \) and the direction vector \( (-1, 3) \):

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \mathbf{v} = (-4, 1) \cdot (-1, 3) \]

\[ D_{\mathbf{v}}f(-1, 2) = (-4)(-1) + (1)(3) = 4 + 3 = 7 \]

The result, 7, is the directional derivative of \( f \) at the point \( (-1, 2) \) in the direction of \( \mathbf{v} = (-1, 3) \).

This tells us that, starting at the point \( (-1, 2, f(-1, 2)) = (-1, 2, 3) \) and moving in the direction of \( \mathbf{v} \), the function increases at a rate of 7 - meaning we're heading uphill.

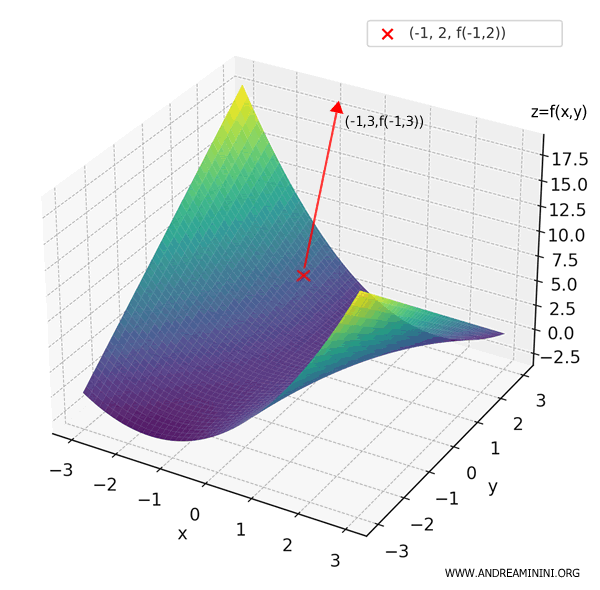
To normalize the directional derivative, we divide the dot product by the magnitude of the direction vector \( \mathbf{v} = (-1, 3) \):

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{v} }{ || \mathbf{v} ||} = \frac{ (-4, 1) \cdot (-1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{v}}f(-1, 2) = \frac{ 4 + 3 }{ \sqrt{10}  } = \frac{7}{\sqrt{10}} \approx 2.21 \]

Note: The direction in which the function increases most rapidly is given by the gradient vector itself, \( (-4, 1) \). So, to ascend as steeply as possible, we should move in the direction of the gradient. \[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \nabla f(-1, 2) }{ || \nabla f(-1, 2) ||} = \frac{ (-4, 1) \cdot (-4, 1) }{ \sqrt{(-4)^2+1^2} } \] \[ D_{\mathbf{v}}f(-1, 2) = \frac{ 16 + 1 }{ \sqrt{17} } = \frac{17}{\sqrt{17}} = \sqrt{17} \approx 4.12 \]

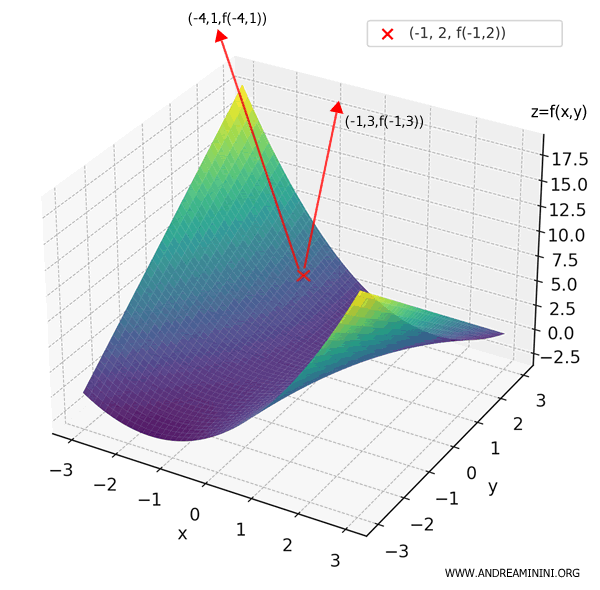
Now, what if we move in a different direction, say \( \mathbf{w} = (1, 3) \), instead of \( \mathbf{v} = (-1, 3) \)?

The gradient we calculated earlier remains the same:

\[ \nabla f(-1, 2) = (-4, 1) \]

We now compute the dot product of the gradient and the new direction vector \( \mathbf{w} = (1, 3) \):

\[ D_{\mathbf{w}}f(-1, 2) = (-4, 1) \cdot (1, 3) = (-4)(1) + (1)(3) = -4 + 3 = -1 \]

The directional derivative is negative, which means \( D_{\mathbf{w}}f(-1, 2) = -1 \). So, moving from \( (-1, 2) \) in the direction \( (1, 3) \), the function decreases.

In other words, we’re heading downhill along the surface of the function.

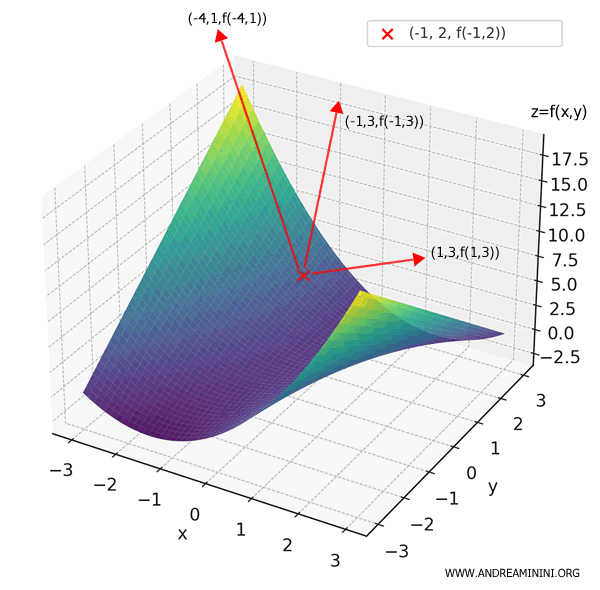
Finally, let’s compute the normalized directional derivative in this direction as well:

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{v} }{ || \sqrt{ \mathbf{v} } ||}  = \frac{ (-4, 1) \cdot (1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{v}}f(-1, 2) = \frac{ -4 + 3 }{ \sqrt{10} } = \frac{ -1 }{ \sqrt{10} } \approx -0.316 \]

This allows us to directly compare the normalized directional rates of change.

Notes

Additional insights and clarifying remarks.

• The connection between directional and partial derivatives

  The partial derivative of \( f \) with respect to \( x_k \) at the point \( \vec{x}_0 \) corresponds to the \(k\)th component of the gradient of \( f \) evaluated at that point.

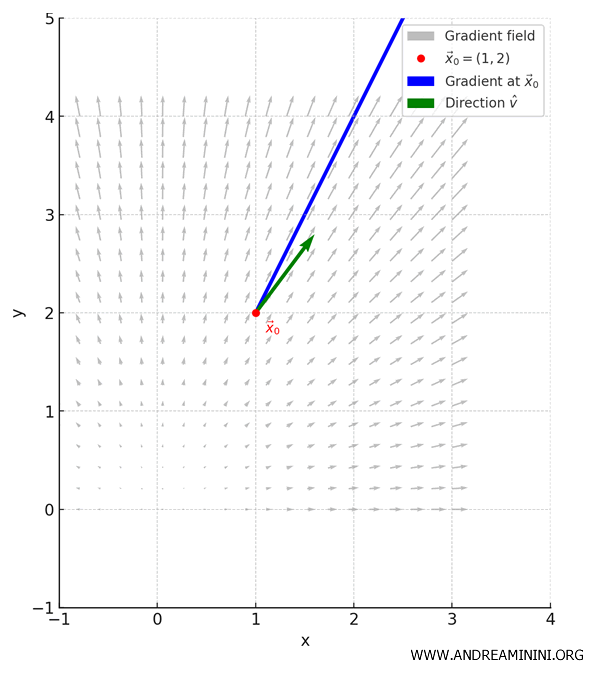
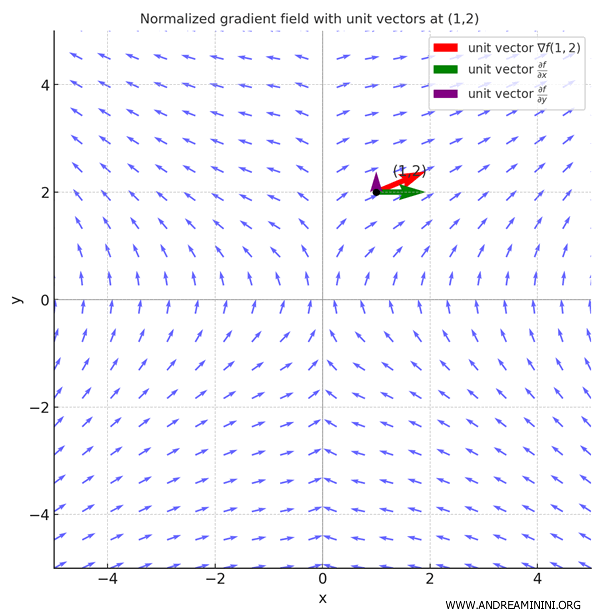
  In other words, partial derivatives are a special case of directional derivatives, where the direction vector \( \vec{v} \) is aligned with one of the standard basis vectors - that is, \( \vec{e}_k \), the unit vector with a 1 in the \(k\)th position and 0 elsewhere. For example, in \( \mathbb{R}^3 \): \[ \vec{e}_1 = (1, 0, 0), \quad \vec{e}_2 = (0, 1, 0), \quad \vec{e}_3 = (0, 0, 1) \] How does this relate to partial derivatives? The partial derivative with respect to \( x_k \) can be expressed as a directional derivative along \( \vec{e}_k \): \[ \frac{\partial f}{\partial x_k}(\vec{x}_0) = \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) \] By the definition of the directional derivative: \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \vec{\alpha} \cdot \vec{e}_k \] where \( \vec{\alpha} = \nabla f(x_0) \) is the gradient vector. Here's the key point: taking the dot product with \( \vec{e}_k \) isolates the \(k\)th component of the gradient: \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \vec{\alpha} \cdot \vec{e}_k = \alpha_k \] Thus, the partial derivative of \( f \) with respect to \( x_k \) at \( \vec{x}_0 \) is precisely the \(k\)th component of the gradient at that point. That is, given a partial derivative \( \frac{\partial f}{\partial x_k} \) and a directional derivative \( \frac{\partial f}{\partial \vec{v}} \), if \( \vec{v} = \vec{e}_k \), then the two derivatives coincide.

  Example. Consider the function: \[ f(x, y) = 3x^2y + 2y \] The partial derivatives are: \[ \frac{\partial f}{\partial x} = 6xy, \quad \frac{\partial f}{\partial y} = 3x^2 + 2 \] Hence, the gradient is: \[ \nabla f(x, y) = \left( 6xy,\ 3x^2 + 2 \right) \] Evaluating the gradient at the point \( (1, 2) \), we obtain: \[ \nabla f(1, 2) = (6 \cdot 1 \cdot 2,\ 3 \cdot 1^2 + 2) = (12,\ 5) \] The partial derivative with respect to \( x \) at \( (1, 2) \) is: \[ \frac{\partial f}{\partial x}(1, 2) = 6 \cdot 1 \cdot 2 = 12 \] Now consider the directional derivative along \( \vec{e}_1 = (1, 0) \). Using the formula: \[ \frac{\partial f}{\partial \vec{e}_1}(1, 2) = \nabla f(1, 2) \cdot \vec{e}_1 = (12,\ 5) \cdot (1,\ 0) = 12 \] This confirms that the partial derivative is equivalent to the directional derivative taken in the direction of the canonical basis vector \( \vec{e}_1 \): \[ \frac{\partial f}{\partial x}(1, 2) = 12 \quad \text{and} \quad \nabla f(1, 2) \cdot \vec{e}_1 = 12 \] The image below illustrates the vector field of normalized gradient vectors.
  

• The gradient is a vector pointing in the direction of greatest increase

  The gradient \( \nabla f(x_0) \) is a vector that points in the direction where the function increases most rapidly.

  The magnitude of the gradient indicates how fast the function is increasing in that direction.

  Proof. We begin with the formula for the directional derivative of \( f \) at the point \( x_0 \) in the direction of a vector \( \vec{v} \). This derivative is given by the dot product of the gradient of \( f \) at that point with the direction vector \( \vec{v} \): \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] Since this is a dot product, we can rewrite it as the product of the magnitudes of the two vectors and the cosine of the angle \( \theta \) between them: \[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \] This expression shows that the directional derivative depends on the magnitude of the gradient \( |\nabla f(x_0)| \), the length of the direction vector \( |\vec{v}| \) (which is typically normalized so that \( |\vec{v}| = 1 \)), and - most importantly - on the cosine of the angle \( \theta \) between \( \nabla f \) and \( \vec{v} \). Understanding how the cosine behaves is the key to interpreting this formula.

  • When \( \cos \theta = 1 \), i.e. \( \theta = 0^\circ \), the two vectors are aligned. The directional derivative is therefore maximal in the direction of the gradient.
  • When \( \cos \theta = -1 \), i.e. \( \theta = 180^\circ \), the vectors point in opposite directions. The directional derivative is then minimal in the opposite direction to the gradient.
  • When \( \cos \theta = 0 \), i.e. \( \theta = 90^\circ \), the vectors are orthogonal. In this case, the directional derivative is zero, meaning the function does not vary in that direction.

  This confirms that the gradient \( \nabla f(x_0) \) points in the direction of steepest ascent, and its magnitude reflects the rate at which the function increases in that direction.

Further examples and insights could be developed along similar lines.

And that’s how it works.