Bounded Set in R² (the Plane)

A set $ A $ in the Cartesian plane $ \mathbb{R}^2 $ is called a bounded set if there exists a sufficiently large circle centered at the origin (i.e., the point $ (0,0) $) that can completely enclose the set $ A $.

This means there is a number $ M > 0 $ such that, for every point $ (x,y) $ in the set $ A $, the distance from these points to the origin, calculated as $ \sqrt{x^2 + y^2} $, is always less than or equal to $ M $.

$$ \sqrt{x^2 + y^2} \le M $$

In other words, $ A $ is contained within a circle of radius $ M $ centered at the origin.

If such an $ M $ can be found, then the set $ A $ is bounded.

If no such $ M $ exists, then $ A $ is unbounded.

A Practical Example

Consider a set of points in the Cartesian plane, for example, a set $ A $ consisting of the points $ A = \{ (1, 2), (2, 3), (3, 1), (1, -1) \} $.

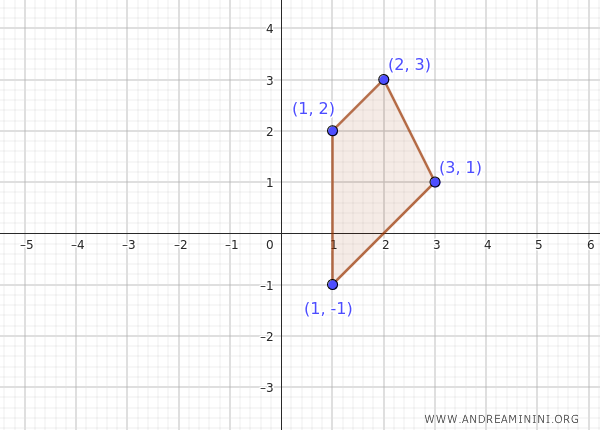
A practical example of a finite set

Now, let’s determine whether this set is bounded.

To do this, we need to check if there exists a circle centered at the origin that can enclose all the points in the set $ A $.

We calculate the distance from the origin for each point in the set $ A $:

For the point $ (1, 2) $: $$ \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \approx 2.24 $$
For the point $ (2, 3) $: $$ \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.61 $$
For the point $ (3, 1) $: $$ \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10} \approx 3.16 $$
For the point $ (1, -1) $: $$ \sqrt{1^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41 $$

Among these distances, the largest is $ \sqrt{13} \approx 3.61 $.

This means that all the points in the set $ A $ can be enclosed within a circle of radius $ M = \sqrt{13} \approx 3.61 $ centered at the origin.

$$ \sqrt{ x^2 + y^2 } \le \sqrt{13} $$

Since such a radius $ M $ exists, we can conclude that the set $ A $ is bounded.

In other words, all the points in $ A $ can be enclosed within a circle centered at the origin with a radius of $ \sqrt{13} $.

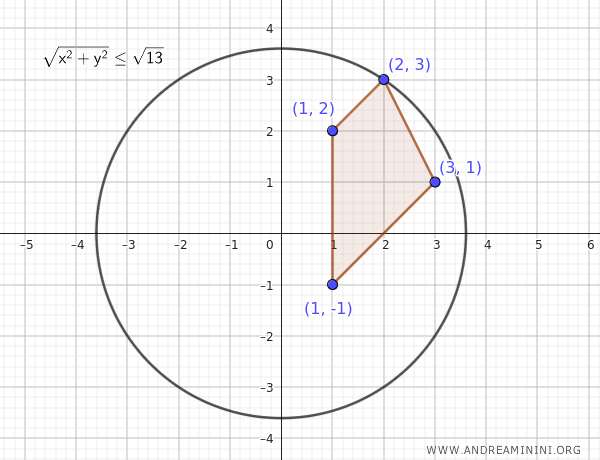
Example of a bounded set

This is a practical example illustrating how to determine whether a set of points in the plane is bounded.

Note: If we consider a set with points that extend infinitely far from the origin, such as all the points along a line that does not pass through the origin, it would be impossible to find a circle that contains all of them, and the set would be unbounded.

And so forth.