Graph of the Functions of Two or More Variables

What Are Multivariable Functions?

Functions of two or more variables involve multiple independent inputs. $$f:R^n \rightarrow R$$

The output can be a single real value (R), an ordered pair (R²), or an m-tuple of real values (R^m).

$$f:R^n \rightarrow R^m$$

Illustrative Examples

Example 1

Consider a function of two real variables:

$$f:R^2 \rightarrow R$$

One such example is:

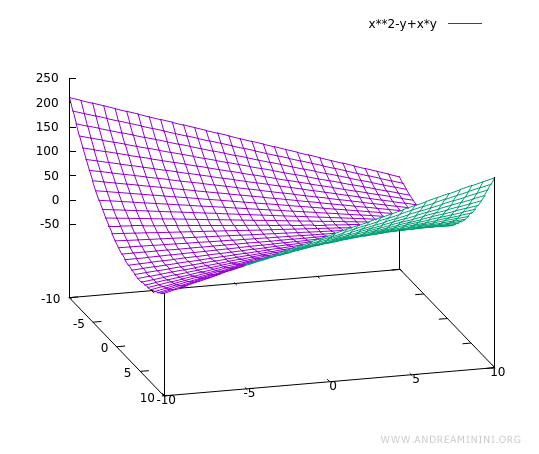
$$f(x,y) = x^2 - y + xy$$

Note. The independent variables can also be written as components of a vector, with $x_1$ and $x_2$ representing the first and second components respectively: $$f(x_1,x_2) = x_1^2 - x_2 + x_1 x_2$$

Below is the graph of the function in three-dimensional space, with axes x, y, and f(x, y):

 

Example 2

Another function of two real variables:

$$f:R^2 \rightarrow R$$

is defined as:

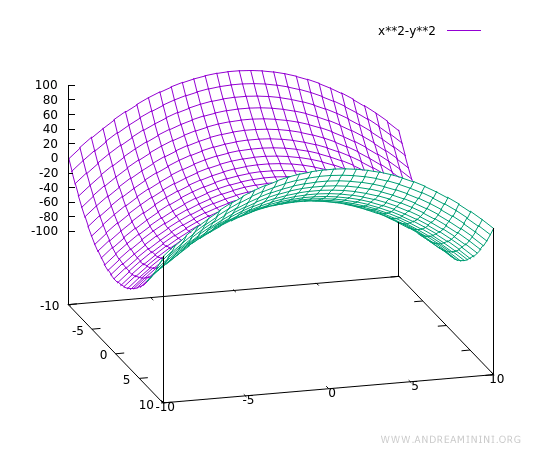
$$f(x,y) = x^2 - y^2$$

Here is its graph in the three-dimensional space (x, y, f(x, y)):

Example 3

Now consider a function of three real variables:

$$f:R^3 \rightarrow R$$

defined as:

$$f(x,y,z) = x^2 + z^2 + yz$$

Note. A function may be defined over multiple variables without necessarily using all of them in its expression. For instance, the function below is still a function of three variables, even though only x and y appear explicitly: $$f(x,y,z) = x^2 + y^2$$

In this case, the graph cannot be visualized, as it resides in four-dimensional space: x, y, z, and f(x, y, z).

The Graph of a Function of Two Variables

The graph of a function $f:A \rightarrow \mathbb{R}$, where $A \subseteq \mathbb{R}^2$, is the set of all points $(x, y, z) \in \mathbb{R}^3$ such that $(x, y)$ lies in the domain $D_f$, and $z = f(x, y)$.

$$\text{graph} = \{ (x, y, z) \in \mathbb{R}^3 \mid (x, y) \in D_f, \ z = f(x, y) \}$$

Here, $\mathbb{R}^3$ is the Cartesian product $\mathbb{R} \times \mathbb{R} \times \mathbb{R}$ of the variables x, y, and z.

Note. For a function of a single variable, the graph is a curve in the plane: $$\text{graph} = \{ (x, y) \in \mathbb{R}^2 \mid x \in D_f, \ y = f(x) \}$$ For a function of two variables, $z = f(x, y)$, the graph becomes a surface in three-dimensional space: $$\text{graph} = \{ (x, y, z) \in \mathbb{R}^3 \mid (x, y) \in D_f, \ z = f(x, y) \}$$

In general, the graph of a function of $n$ variables is a subset of $\mathbb{R}^{n+1}$ and is defined as follows:

$$\text{graph} = \{ (\vec{x}, y) \in \mathbb{R}^{n+1} \mid \vec{x} \in D_f, \ y = f(\vec{x}) \}$$

Here, $\vec{x}$ is a vector with $n$ components, and $y$ is a real number.

$$\vec{x} = (x_1, x_2, \ldots, x_n)$$

Note. This notation closely mirrors the one-variable case, $y = f(x)$, where $x$ is a real number: $$\text{graph} = \{ (x, y) \in \mathbb{R}^2 \mid x \in D_f, \ y = f(x) \}$$ In a multivariable context, however, $x$ becomes a vector in $\mathbb{R}^n$: $$\text{graph} = \{ (\vec{x}, y) \in \mathbb{R}^{n+1} \mid \vec{x} \in D_f, \ y = f(\vec{x}) \}$$

And so on.