Differentiability of a Function of Two Variables

Let \( f: \mathbb{R}^2 \to \mathbb{R} \) be a real-valued function of two variables. We say that \( f \) is differentiable at the point \( (x_0, y_0) \in \mathbb{R}^2 \) if there exist two real numbers \( \alpha \) and \( \beta \) such that: \[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \] 

Here:

• \( h \) and \( k \) represent small displacements along the \( x \)- and \( y \)-axes
• \( \sqrt{h^2 + k^2} \) is the Euclidean distance between the point \( (x_0, y_0) \) and the perturbed point \( (x_0 + h, y_0 + k) \)
• \( o\left(\sqrt{h^2 + k^2}\right) \) denotes a higher-order infinitesimal - an error term that vanishes faster than the displacement itself

If \( f \) is differentiable at \( (x_0, y_0) \), then its partial derivatives exist at that point and satisfy:

\[ \alpha = \frac{\partial f}{\partial x}(x_0, y_0) \]

\[ \beta = \frac{\partial f}{\partial y}(x_0, y_0) \]

This means the differentiability formula can be rewritten as:

\[ f(x_0 + h, y_0 + k) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot h + \frac{\partial f}{\partial y}(x_0, y_0) \cdot k + o\left(\sqrt{h^2 + k^2}\right) \]

Recall that the gradient of \( f \) at the point \( (x_0, y_0) \) is composed of the partial derivatives evaluated at that point:

\[ \nabla f(x_0, y_0) = \left( \frac{\partial f}{\partial x}(x_0, y_0),\ \frac{\partial f}{\partial y}(x_0, y_0) \right) \]

Using this, the first-order approximation of the function at a nearby point \( (x_0 + h,\ y_0 + k) \) can be written as:

\[ f(x_0 + h,\ y_0 + k) = f(x_0,\ y_0) + \nabla f(x_0,\ y_0) \cdot (h,\ k) + o\left( \sqrt{h^2 + k^2} \right) \]

If we now express the displacement vector as \( \vec{h} = (h,\ k) \) and the reference point as \( \vec{x}_0 = (x_0,\ y_0) \), the same expression takes a cleaner, more compact vector form:

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \nabla f(\vec{x}_0) \cdot \vec{h} + o(\|\vec{h}\|) \]

In intuitive terms, a function \( f(x, y) \) is differentiable at a point if, in a neighborhood around that point, it behaves almost like a plane.

In other words, the function can be locally approximated by a tangent plane.

This is a significantly stronger condition than the mere existence of partial derivatives, and it ensures that the function behaves smoothly near that point.

Note. The symbol \( o\left(\sqrt{h^2 + k^2}\right) \) encodes the following limit: \[ \lim_{(h, k) \to (0, 0)} \frac{o\left(\sqrt{h^2 + k^2}\right)}{\sqrt{h^2 + k^2}} = 0 \] This means the error term becomes negligible compared to \( \sqrt{h^2 + k^2} \) as the point \((h, k)\) approaches \((0, 0)\). This condition guarantees that the local behavior of the function is linear to a first approximation.

How do you determine whether a function is differentiable at a point?

In practice, the total differential theorem is the go-to tool for assessing differentiability at a point, as it offers a far more practical and elegant alternative to the often cumbersome formal definition.

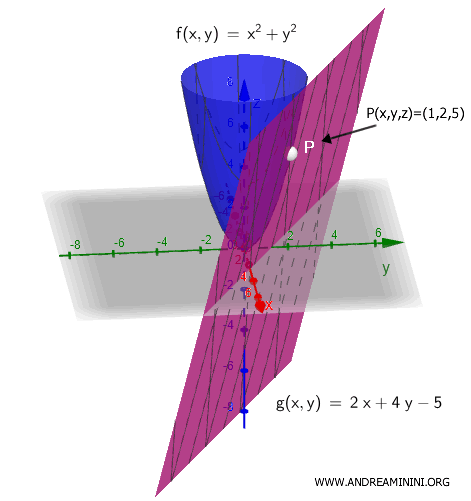
A Practical Example

Consider the function:

\[ f(x, y) = x^2 + y^2 \]

We want to determine whether this function is differentiable at the point \( (x_0, y_0) = (1, 2) \).

Substituting these coordinates into the differentiability formula gives:

\[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

\[ f(1 + h,\ 2 + k) = f(1, 2) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Since \( f(1, 2) = 1^2 + 2^2 = 5 \), we get:

\[ f(1 + h,\ 2 + k) = 5 + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Here, \(\alpha\) and \(\beta\) are the partial derivatives of the function at \( (1, 2) \):

\[ \alpha = \frac{\partial f}{\partial x}(1, 2) = 2x = 2 \cdot 1 = 2 \]

\[ \beta = \frac{\partial f}{\partial y}(1, 2) = 2y = 2 \cdot 2 = 4 \]

Note. The values \(\alpha\) and \(\beta\) are precisely the coefficients of the tangent plane at the point \((x_0, y_0)\). They indicate the direction and rate of change of the surface, just as a tangent line does in single-variable calculus.

So, the coefficients of the tangent plane at \( (x_0, y_0) = (1, 2) \) are \( \alpha = 2 \) and \( \beta = 4 \):

\[ f(1 + h, 2 + k) = 5 + 2h + 4k + o\left(\sqrt{h^2 + k^2}\right) \]

Now consider small displacements \( h \) and \( k \) from the point \( (1, 2) \).

For example, if \( h = 0.01 \) and \( k = -0.02 \), the linear approximation gives:

\[ f(1.01, 1.98) \approx 5 + 2 \cdot 0.01 + 4 \cdot (-0.02) = 5 + 0.02 - 0.08 = 4.94 \]

The higher-order term \( o(\cdot) \) is negligible, so we omit it.

The actual function value is very close to 4.94, with only a negligible error (4.94 ≈ 5).

What is the equation of the tangent plane?

The general formula for the tangent plane is:

\[ z = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot (x - x_0) + \frac{\partial f}{\partial y}(x_0, y_0) \cdot (y - y_0) \]

Given that \( (x_0, y_0) = (1, 2) \) and \( f(1, 2) = 5 \), we have:

\[ z = 5 + \frac{\partial f}{\partial x}(1, 2) \cdot (x - 1) + \frac{\partial f}{\partial y}(1, 2) \cdot (y - 2) \]

The partial derivatives are \( \frac{\partial f}{\partial x}(1, 2) = 2 \) and \( \frac{\partial f}{\partial y}(1, 2) = 4 \), so:

\[ z = 5 + 2(x - 1) + 4(y - 2) \]

\[ z = 5 + 2x - 2 + 4y - 8 \]

\[ z = 2x + 4y - 5 \]

This is the equation of the plane \( g(x, y) = 2x + 4y - 5 \), which locally approximates the surface of the function \( f(x, y) = x^2 + y^2 \) at the point \( P(x_0, y_0, z) = (1, 2, 5) \).

Differentiability in Functions of n Variables

Differentiability in \( \mathbb{R}^n \) is more elegantly expressed using vector notation:

A function \( f : \mathbb{R}^n \to \mathbb{R} \) is differentiable at a point \( \vec{x}_0 \in \mathbb{R}^n \) if there exists a vector \( \vec{\alpha} \in \mathbb{R}^n \) such that: \[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(\|\vec{h}\|) \quad \text{as } \vec{h} \to \vec{0} \]

Where:

• \( \vec{x}_0 \) is the position vector of the fixed point where we want to study differentiability
• \( \vec{h} \) is the increment vector - i.e., a displacement from \( \vec{x}_0 \)
• \( \vec{\alpha} \) is the gradient of the function at \( \vec{x}_0 \)
• \( \vec{\alpha} \cdot \vec{h} \) is the dot product, representing the linear part of the approximation
• \( o(\|\vec{h}\|) \) is the error term that vanishes faster than \( \|\vec{h}\| \)

The condition \( \vec{h} \to \vec{0} \) means that we approach \( \vec{x}_0 \) from all possible directions.

If \( f \) is differentiable at \(\vec{x}_0 \), then all \( n \) partial derivatives exist at that point.

How is a directional derivative computed?

If a function \( f \) is differentiable at a point \( \vec{x}_0 \), then the directional derivative of \( f \) in the direction of a vector \( \vec{v} \) is given by the dot product of the gradient of \( f \) at that point and the direction vector \( \vec{v} \).

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \]

In this expression, \( \vec{v} \) is the direction vector, and \( \vec{\nabla}f(x_0) \) denotes the gradient of the function at the point \(\vec{x}_0\).

Total Differential Theorem

Let \( f(x, y) \) be a function defined in a neighborhood of a point \( (x_0, y_0) \in \mathbb{R}^2 \). If the partial derivatives \( f_x \) and \( f_y \) exist throughout a neighborhood of \( (x_0, y_0) \) and are continuous at that point, then \( f \) is differentiable at \( (x_0, y_0) \).

Under these conditions, the total differential of \( f \) at \( (x_0, y_0) \) is given by:

\[ df = f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy \]

This provides a linear approximation of the function near the point:

\[ f(x, y) \approx f(x_0, y_0) + f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0) \]

The total differential theorem is a powerful tool because it allows us to establish differentiability at a point without having to resort to the formal definition, which is often more intricate and technically demanding.

Note. This theorem offers a sufficient - but not necessary - condition for differentiability. That is, if the partial derivatives exist in a neighborhood of a point and are continuous at that point, then the function is differentiable there. However, it’s still possible for a function to be differentiable at a point even if its partial derivatives fail to be continuous there.

Example

Let’s revisit the function from the previous example:

\[ f(x, y) = x^2 + y^2 \]

We’ll verify that \( f \) is differentiable at the point \( (1, 2) \) by applying the total differential theorem.

The partial derivatives of the function are:

\[ f_x(x, y) = \frac{\partial}{\partial x}(x^2 + y^2) = 2x \\ f_y(x, y) = \frac{\partial}{\partial y}(x^2 + y^2) = 2y \]

Since both \( f_x(x, y) = 2x \) and \( f_y(x, y) = 2y \) are polynomials, they are continuous everywhere in \( \mathbb{R}^2 \).

Therefore, the partial derivatives are continuous in a neighborhood of \( (1, 2) \).

By the total differential theorem, it follows that the function is differentiable at \( (1, 2) \), since the partial derivatives exist and are continuous there.

For completeness, we can also compute the total differential of the function at \( (1, 2) \):

\[ df = f_x(1, 2) \, dx + f_y(1, 2) \, dy = 2 \cdot 1 \cdot dx + 2 \cdot 2 \cdot dy = 2dx + 4dy \]

This gives us a quick and reliable way to determine whether a function is differentiable at a point, without relying on the formal definition.

Note. In this particular case, the continuity of the partial derivatives is obvious, since they are polynomial functions. More generally, though, verifying the continuity of a partial derivative requires showing that its limit exists and equals its value at the point of interest. For instance, if \( f_x(x, y) = 2x \), then we consider: \[ \lim_{(x,y) \to (1,2)} 2x = 2 \cdot 1 = 2 \] which agrees with the actual value at the point: \[ f_x(1,2) = 2 \cdot 1 = 2 \] In the plane - or in higher dimensions - a limit exists only if it converges to the same value along all possible paths approaching the point. Verifying this directly is practically impossible. That’s why we use the method of translated polar coordinates, which provides a more systematic and rigorous approach for examining the behavior of the function from all directions. To study the behavior near \( (1, 2) \), we shift the origin by applying the following change of coordinates: \[ x = 1 + r \cos\theta,\quad y = 2 + r \sin\theta \] Substituting into the partial derivative: \[ f_x(x, y) = 2x = 2(1 + r \cos\theta) = 2 + 2r \cos\theta \] We then take the limit as \( r \to 0 \): \[ \lim_{r \to 0} f_x(x, y) = \lim_{r \to 0} \left(2 + 2r \cos\theta\right) = 2 \] This limit is independent of \( \theta \), meaning it does not depend on the direction from which we approach the point, and it coincides with the value of the partial derivative at the point: \[ f_x(1, 2) = 2 \cdot 1 = 2 \] Hence, the limit exists, is direction-independent, and matches the value of the partial derivative at the point. We can conclude that \( f_x(x, y) = 2x \) is continuous at \( (1, 2) \). Naturally, the same verification should be performed for the other partial derivative \( f_y(x,y) \) as well.

Differentiability Theorem

In essence, if a function is differentiable at a point, it must also be continuous there, possess all partial derivatives, and its directional derivatives in any direction are obtained via a dot product with the gradient.

However, the converse of this theorem does not hold: the implication is one-way.

There exist functions for which all partial derivatives exist at a point \( \vec{x}_0 \), yet the function fails to be continuous - and hence is not differentiable - at that point.

Example

Consider the function of two variables defined by:

\[ f(x, y) = \begin{cases} \displaystyle \frac{xy}{x^2 + y^2} & \text{if } (x, y) \neq (0, 0) \\ 0 & \text{if } (x, y) = (0, 0) \end{cases} \]

Let’s compute the partial derivatives at a generic point \((x, y)\):

The partial derivative with respect to \( x \) is:

\[ \frac{\partial f}{\partial x}(x, y) = \frac{(x^2 + y^2) \cdot y - 2x \cdot xy}{(x^2 + y^2)^2} = \frac{y(-x^2 + y^2)}{(x^2 + y^2)^2} \]

The partial derivative with respect to \( y \) is:

\[ \frac{\partial f}{\partial y}(x, y) = \frac{(x^2 + y^2) \cdot x - 2y \cdot xy}{(x^2 + y^2)^2} = \frac{x(x^2 - y^2)}{(x^2 + y^2)^2} \]

Thus, at any point \((x, y)\), the partial derivatives are:

\[ \frac{\partial f}{\partial x}(x, y) = \frac{y(-x^2 + y^2)}{(x^2 + y^2)^2} \]

\[ \frac{\partial f}{\partial y}(x, y) = \frac{x(x^2 - y^2)}{(x^2 + y^2)^2} \]

Now, let’s examine the behavior of \( f \) at the origin.

At \( (0,0) \), both partial derivatives exist.

The partial derivative with respect to \( x \) is:

\[ \frac{\partial f}{\partial x}(x, 0) = \frac{0(0^2 - x^2)}{(x^2 + 0^2)^2} = 0 \]

And similarly, the partial derivative with respect to \( y \) is:

\[ \frac{\partial f}{\partial y}(0, y) = \frac{0(0^2 - y^2)}{(0^2 + y^2)^2} = 0 \]

So both partial derivatives at the origin are well-defined and equal to zero.

Next, let’s investigate the limit of the function as we approach \( (0,0) \) from different directions.

Consider the directional derivative along the line \( y = x \), i.e., in the direction \( \vec{v} = (1, 1) \):

\[ D_{\vec{v}}f(0,0) = \lim_{h \to 0} \frac{f(h, h) - f(0,0)}{h} \]

We compute: \( f(h, h) = \frac{h^2}{2h^2} = \frac{1}{2} \), while \( f(0, 0) = 0 \):

\[ D_{\vec{v}}f(0,0) = \lim_{h \to 0} \frac{1/2 - 0}{h} = \lim_{h \to 0} \frac{1}{2h} = \pm \infty \]

This limit does not exist, as it diverges to \( +\infty \) when \( h \to 0^+ \) and to \( -\infty \) when \( h \to 0^- \).

Even though the function approaches 0 along the x- and y-axes, continuity requires the limit to exist and be the same regardless of the path taken.

Since the limit along the line \( y = x \) does not exist, we conclude that the function is not continuous at the origin.

Therefore, it is not differentiable at that point.

Note. To prove that \( \frac{xy}{x^2 + y^2} \) is not continuous at \( (0,0) \), it suffices to observe that the function approaches different values depending on the path. Along the x-axis (\( y = 0 \)), the function is identically zero: \[ \lim_{x \to 0} f(x, 0) = \lim_{x \to 0} \frac{x \cdot 0}{x^2 + 0^2} = 0 \] But along the line \( y = x \), we have: \[ \lim_{x \to 0} f(x, x) = \lim_{x \to 0} \frac{x^2}{2x^2} = \frac{1}{2} \] This discrepancy is enough to conclude that the function is not continuous at \( (0,0) \).

To summarize: the function admits partial derivatives at \( (0,0) \), and they are both zero, but its limiting behavior depends on the direction of approach.

This is a classic example of a function that, despite having partial derivatives (which are zero) at a point, fails to be continuous - and hence differentiable - there.

It clearly illustrates that the converse of the differentiability theorem does not hold.

Example 2

In this example, we examine a function of two variables:

\[ f(x,y) =  \begin{cases} \left( \frac{x^2 y}{x^4 + y^2} \right)^2 & \text{if } (x,y) \neq (0,0) \\ 0 & \text{if } (x,y) = (0,0)
\end{cases} \]

To determine whether \(f\) is continuous at \((0,0)\), we need to verify whether

\[ \lim_{(x,y) \to (0,0)} f(x,y) = f(0,0) = 0 \]

However, if we approach the origin along the parabola \(y = x^2\) - that is, by letting \(x = t,\; y = t^2\) - we obtain:

\[ f(t, t^2) = \left( \frac{t^2 \cdot t^2}{t^4 + t^4} \right)^2 = \left( \frac{t^4}{2t^4} \right)^2 = \left( \frac{1}{2} \right)^2 = \frac{1}{4} \]

So the limit along this path is \(1/4\), while \(f(0,0) = 0\).

Since the limit depends on the path taken, it does not exist in the general sense. Therefore, the function is not continuous at (0,0).

Next, we investigate whether the directional derivatives at \((0,0)\) exist, and if so, what their values are.

The directional derivative in the direction of a general vector \(\vec{v} = (\alpha, \beta)\) at the origin is given by:

\[ \lim_{t \to 0} \frac{f(t\alpha, t\beta) - f(0,0)}{t} = \lim_{t \to 0} \frac{f(t\alpha, t\beta)}{t} \]

Let’s compute this expression:

\[ f(t\alpha, t\beta) = \left( \frac{(t\alpha)^2 \cdot t\beta}{(t\alpha)^4 + (t\beta)^2} \right)^2 = \left( \frac{t^3 \alpha^2 \beta}{t^4 \alpha^4 + t^2 \beta^2} \right)^2 \]

Therefore, we have:

\[
\begin{aligned}
\frac{f(t\alpha,t\beta)}{t}
&=\frac1t\left(
\frac{t^{3}\alpha^{2}\beta}{t^{4}\alpha^{4}+t^{2}\beta^{2}}
\right)^{2}\\[6pt]
&=\frac1t\left(
\frac{t\,\alpha^{2}\beta}{t^{2}\alpha^{4}+\beta^{2}}
\right)^{2}\\[6pt]
&=\frac1t\,
\frac{t^{2}\alpha^{4}\beta^{2}}
{(t^{2}\alpha^{4}+\beta^{2})^{2}}\\[6pt]
&=\frac{t\,\alpha^{4}\beta^{2}}
{(t^{2}\alpha^{4}+\beta^{2})^{2}}.
\end{aligned}
\]

As \(t \to 0\), the numerator tends to zero linearly with \(t\), while the denominator approaches \(\beta^4\). Hence, the entire expression approaches zero.

\[ \lim_{t \to 0} \frac{f(t\alpha, t\beta)}{t} = \lim_{t \to 0} \frac{t\,\alpha^{4}\beta^{2}}{(t^{2}\alpha^{4} + \beta^{2})^2} = 0 \]

Thus, every directional derivative at \((0,0)\) exists and is equal to 0.

This example shows that although all directional derivatives at the origin exist and vanish, the function is still not continuous at that point.

As a result, the function is not differentiable at \((0,0)\), even though all directional derivatives exist.

In conclusion, the existence of all directional derivatives - even when they are zero - is not sufficient to guarantee continuity or differentiability.

And so on.