Open Ball (or Spherical Neighborhood)

An open ball (also called an open spherical neighborhood) is the set of all points whose distance from a fixed point \( x \) is less than a given radius \( r \): \[ B_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| < r \} \] Here, \( x \) is the center of the ball, \( r > 0 \) is the radius, and \( \|y - x\| \) denotes the distance between \( y \) and \( x \) - usually the Euclidean distance.

In mathematics, the open ball is a key concept for understanding what it means for a point to be “close to” another in a space.

A ball is called "open" when it doesn’t include the boundary, and "closed" when it does.

Open balls provide the foundation for important ideas such as continuity, convergence, and open sets.

Examples

Here are some concrete examples.

Example 1

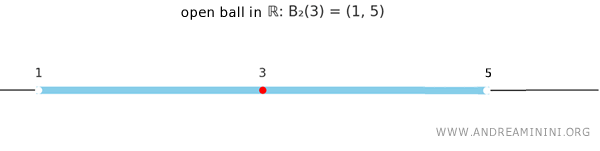
In the real line \( \mathbb{R} \), open balls reduce to open (or closed) intervals.

For example, take the point \( x = 3 \) and radius \( r = 2 \). The corresponding open ball is:

\[ B_2(3) = \{ y \in \mathbb{R} : |y - 3| < 2 \} = (1, 5) \]

This is simply an open interval centered at 3 and spanning 4 units in total.

Example 2

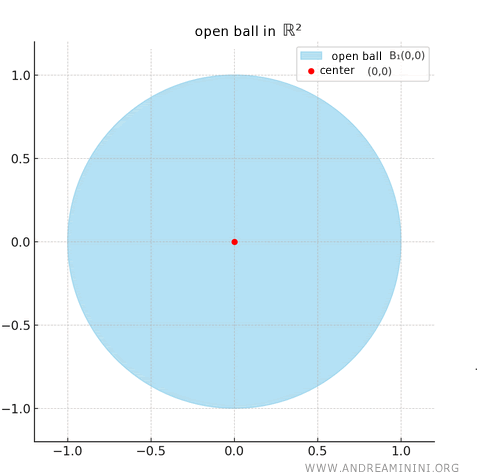
In the plane \( \mathbb{R}^2 \), an open ball takes the shape of an open disk.

For instance, here’s an open ball centered at the origin with radius 1:

\[ B_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} < 1 \} \]

Since the ball is open, the boundary is not included.

Example 3

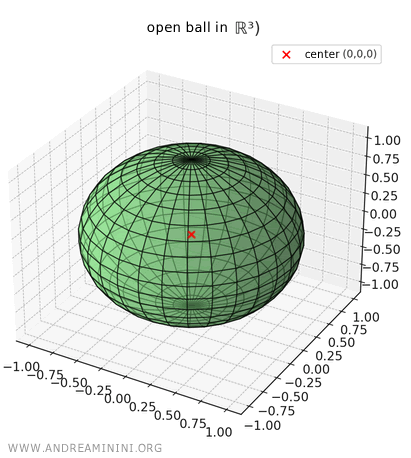
In three-dimensional space \( \mathbb{R}^3 \), an open ball looks like a solid sphere without its surface:

\[ B_1((0, 0, 0)) = \{ (x, y, z) \in \mathbb{R}^3 : \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2} < 1 \} \]

In other words, it's the inside of a sphere, excluding the outer shell.

Because the ball is open, points exactly at a distance of \( r = 1 \) are not part of the set.

Closed Ball (or Closed Spherical Neighborhood)

A closed ball includes the boundary - that is, all points whose distance from the center is less than or equal to \( r \):

\[ \overline{B}_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| \le r \} \]

Put differently, a closed ball consists of the open ball along with the surface of the sphere.

Example

A closed ball centered at the origin in the plane with radius 1 forms a filled circle:

\[ \overline{B}_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} \le 1 \} \]

In this case, the circular boundary is included in the set.

Key Properties of a Ball

A ball - whether open or closed - has the following key properties:

• Centered
  Every ball is centered around a fixed point \( x \), which serves as its reference.
• Symmetric
  A ball is symmetric because only the distance from \( x \) matters - direction is irrelevant.
• Topologically significant
  Balls are fundamental in topology, as they provide a precise way to define the concept of “closeness.”

These three properties hold for all balls, open or closed, regardless of the number of dimensions in the space.

Balls in Non-Euclidean Spaces

Mathematically, balls (or spherical neighborhoods) can be defined in any metric space - not just in Euclidean space.

When distances are measured using a norm other than the Euclidean norm, the shape of the ball changes. However, the core idea remains: it is the set of all points “close to” a center point, within a given radius.

In general, in a metric space, an open ball is defined as:

\[ B_r(x) = \{ y \in X : d(x, y) < r \} \]

Here, \( X \) is the space, \( d(x, y) \) is a general distance function (not necessarily Euclidean), and \( r > 0 \) is the radius.

The shape of a ball depends on the metric or norm used.

For example, under the Euclidean metric, the ball is a circle; under the Manhattan metric, it's a diamond; and so on.

A] Manhattan Distance

Under the Manhattan (or taxicab) metric, the ball is defined as:

\[ \|x - y\|_1 = \sum_{i=1}^n |x_i - y_i| \]

In \( \mathbb{R}^2 \), this results in a diamond-shaped region centered at \( x \), with sides aligned at 45° angles to the axes.

For example, if \( r = 1 \):

\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : |x| + |y| < 1 \} \]

B] Maximum (Chebyshev) Distance

With the maximum metric, the ball is defined by:

\[ \|x - y\|_\infty = \max_i |x_i - y_i| \]

In \( \mathbb{R}^2 \), this produces a square centered at \( x \), with sides parallel to the coordinate axes.

For instance, if \( r = 1 \):

\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : \max(|x|, |y|) < 1 \} \]

C] Discrete Metric Space

In a space equipped with the discrete metric, the ball is defined as follows:

\[ d(x, y) = \begin{cases} 0 & \text{if } x = y \\ 1 & \text{if } x \ne y \end{cases} \]

In this case, an open ball with radius 1 contains only the center point \( x \), since all other points are exactly 1 unit away.

By contrast, the closed ball includes all points in the space.

Example

Consider a finite set \( X = \{a, b, c\} \), with the discrete metric defined as:

\[ d(x, y) =
\begin{cases}
0 & \text{if } x = y \\
1 & \text{if } x \ne y
\end{cases}
\]

An open ball centered at \( a \) with radius 1 includes only the points strictly less than 1 unit away from \( a \).

Since \( d(a, y) < 1 \) only when \( y = a \), we get:

\[ B_1(a) = \{ a \} \]

The closed ball centered at \( a \), however, includes all points with distance less than or equal to 1 - so the entire set:

\[ \overline{B}_1(a) = \{ y \in X : d(a, y) \le 1 \} = \{a, b, c\} = X \]

So in a discrete metric space, an open ball always contains just the center, while a closed ball contains the entire space.

This may seem like an extreme case, but it’s a valuable example for highlighting the distinction between open and closed balls - especially in non-geometric contexts.

And so on.