Types of Functions

There are various types of functions. Here are the main categories:

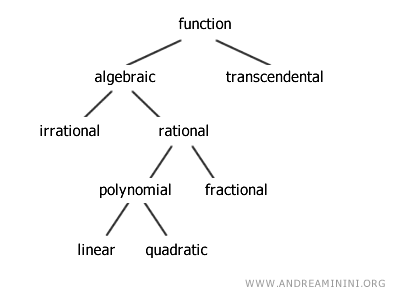
• Algebraic Functions
  A function is classified as algebraic if its expression f(x) involves only the operations of addition, subtraction, multiplication, exponentiation, or taking roots.

  Example. The following are algebraic functions: $$ y=2x^2+x $$ $$ y= \frac{x+1}{x-1} $$ $$ y = x - \sqrt{x} $$

• Transcendental Functions
  A function is said to be transcendental if it is not algebraic.

  Example. Functions involving exponential expressions like \( a^x \), logarithms, or trigonometric functions are transcendental: $$ y=2^x $$ $$ y= \sin(x) $$ $$ y = \log(x) $$

Algebraic functions can be further divided into rational and irrational functions:

• Rational Functions
  A function is called rational if the independent variable x does not appear under a radical.

  Example. Examples of rational functions include: $$ y = x^2+1 $$ $$ y = \frac{2x+1}{x-1} $$ $$ y = x^3-x^2+2 $$

• Irrational Functions
  A function is called irrational if the independent variable x appears under at least one radical.

  Example. Examples of irrational functions include: $$ y = \sqrt{x} $$ $$ y = x - \sqrt{x} $$ $$ y = \frac{ \sqrt{x} }{x+1} $$

Rational functions, in turn, are categorized as either polynomial (also known as whole) functions or rational fractional functions:

• Polynomial (Whole) Functions
  A function is considered a polynomial (or whole) function if its expression f(x) is a polynomial of any degree.
  • Linear Functions
    when the polynomial is of degree 1
  • Quadratic Functions
    when the polynomial is of degree 2

  Example. These are examples of linear polynomial functions: $$ y = 2x+1 $$ $$ y = 5-3x $$ Examples of quadratic polynomial functions: $$ y = x^2-3x+1 $$ $$ y = 3x^2+2x+1 $$ Other polynomial functions that are neither linear nor quadratic: $$ y = 2x^3+x^2-1 $$ $$ y = x^5-3x^3+2 $$

• Rational Fractional Functions
  A function is called a rational fractional function when f(x) is the quotient of two polynomials.

  Example. Examples of rational fractional functions include: $$ y = \frac{x+1}{x-1} $$ $$ y = \frac{x^2+2x-1}{x^3+x^2+4} $$ $$ y = \frac{x^4+x-1}{x^2+3} $$

And so forth.