Periodic Functions

Understanding Periodic Functions

A function is called periodic with period T if $$ f(x+T)=f(x) $$ for every x in R.

A function with period T is also periodic for any multiple of T.

$$ f(x+T) = f(x+kT) = f(x) $$

where k is an integer.

A Practical Example

The cosine function is a classic example of a periodic function, with a period of T=2π.

For example, at x=0 and x=2π, the function f(x) yields the same value.

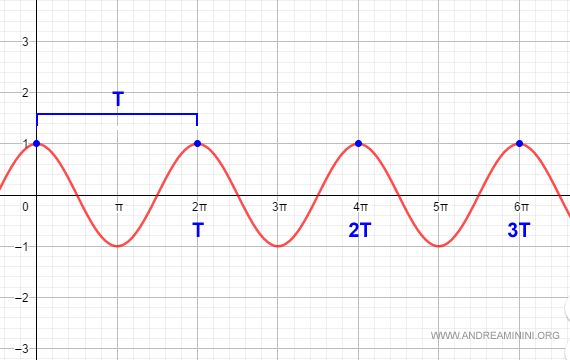
Similarly, at x=4π, the function still takes the same value.

This function consistently repeats its values across its range for each multiple of the period T.

And so on.