Polynomial Functions

What is a polynomial function?

A function is called a polynomial function when its expression is given by a polynomial: $$ y = P(x) $$

Here’s an example of a polynomial function:

$$ f(x) = x^3 - x^2 - 2x + 2 $$

In this case, the function is defined by the polynomial P(x) = x³ - x² - 2x + 2, which is a third-degree polynomial in a single variable.

By substituting various values of the independent variable \( x \) - whose domain here is the set of real numbers - we can compute the corresponding values of the function \( y = f(x) \).

Let’s evaluate the function around the point \( x = 0 \):

$$ \begin{array}{c|lcr} x & \text{y} \\ \hline -3 & -28 \\ -2 & -6 \\ -1 & 2 \\ 0 & 2 \\ 1 & 0 \\ 2 & 2 \\ 3 & 14 \end{array} $$

Each row in the table above shows a pair of coordinates \((x, y)\), representing points on the Cartesian plane.

This information allows us to sketch an approximate graph of the function near the chosen point.

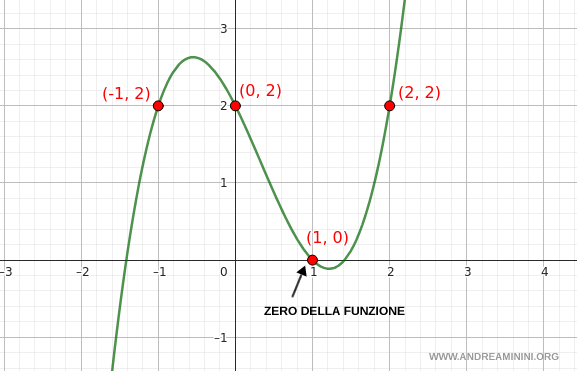
The values of \( x \) for which the function equals zero - that is, \( y(x) = 0 \) - are called the roots or zeros of the polynomial.

At these points, the graph of the function crosses the x-axis, since the output value is \( y = 0 \).

In this example, the function has a single zero at the point \((1, 0)\), which occurs when the independent variable is \( x = 1 \).

Note: A function may have one, several, or no real zeros. On the other hand, the values of \( x \) for which the function grows without bound - either positively or negatively - are known as poles.

And so on.