Odd Functions
What Are Odd Functions?
A function is called odd if for any x in its domain, the following holds: $$ f(-x) = -f(x) \ \ \ \forall \ x \ \in D $$
The graph of an odd function is symmetric about the origin, meaning that for every point P(x, y), there’s an opposite point P(-x, -y).
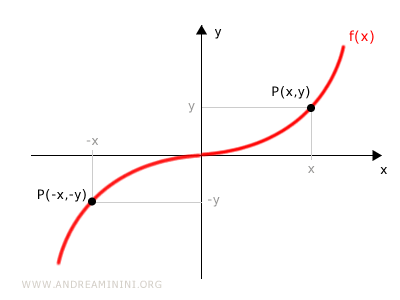
How Can You Tell If a Function Is Odd?
There are two ways to check:
- From an analytical perspective, compare the value of f(-x) with -f(x). If they match, the function is odd. $$ f(-x) = -f(x) $$
Example. Let’s take the function f(x) = x3. Replace x with -x and check if it equals -f(x). $$ f(-x) = (-x)^3 = -x^3 = -f(x) $$ Since f(-x) matches -f(x), the function is odd.
- From a graphical point of view, reflect the graph vertically across the negative x-axis. If the graphs of g(x) and f(x) are symmetric about the origin, then the function is odd.
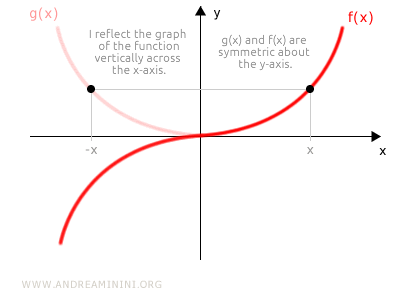
Note. A function doesn’t have to be odd just because it’s not even, and vice versa. For instance, the function f(x) = x + x2 is neither odd $$ f(-x) = (-x) + (-x)^2 = -x + x^2 \ne -f(x) = -x - x^2 $$ nor even. $$ f(-x) = (-x) + (-x)^2 = -x + x^2 \ne f(x) = x + x^2 $$
A Practical Example
A well-known example of an odd function is the sine function.
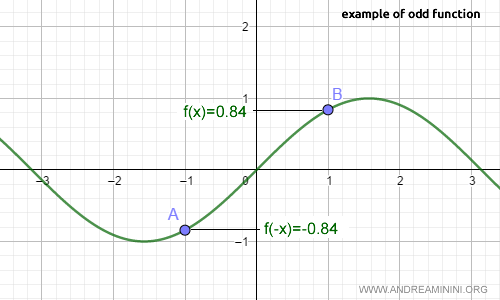
For any x in the domain of the sine function, the relation f(-x) = -f(x) holds.
Note. For example, at x = 1, sin(1) = 0.84. When we evaluate the function at -1, we get sin(-1) = -0.84, the same as -sin(1). So, f(-x) = -f(x).
Example 2
Another example of an odd function is x3.
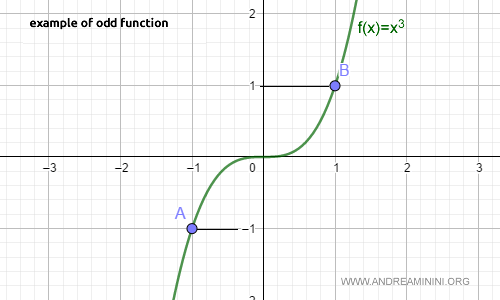
For any x in the function’s domain, the relation f(-x) = -f(x) holds.
Note. In general, if a function only contains powers of x with odd exponents, it is an odd function.
Example 3
Let’s analytically verify if this function is odd:
$$ f(x) = x^2 + x $$
Substitute x with -x in the function expression:
$$ f(-x) = (-x)^2 + (-x) = x^2 - x $$
The result is not the same as -f(x):
$$ -f(x) = -(x^2 + x) = -x^2 - x $$
So, this function is not odd.
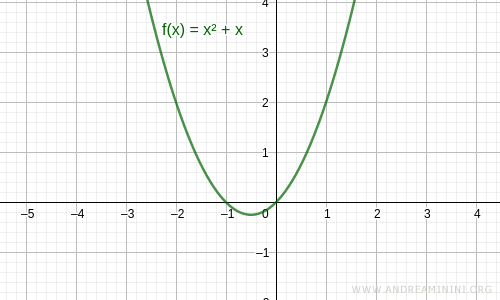
Note. The function f(x) = x2 + x is also not even because it’s not symmetric about the y-axis.
And so on.
