Zeros of a Function

A real number \( x \) is called a zero of the function \( y = f(x) \) if the value of the function at that point is zero: $$ f(x) = 0 $$

From a graphical perspective, the zeros of a function are the points where its graph intersects the x-axis.

A Concrete Example

Consider the following function:

$$ f(x) = x^2 - 4x $$

To find its zeros, we look for the values of \( x \) that make the function equal to zero:

$$ f(x) = 0 $$

This leads us to solve the equation:

$$ x^2 - 4x = 0 $$

This is a quadratic equation, and it can be solved easily by factoring out \( x \):

$$ x(x - 4) = 0 $$

The equation is satisfied when either \( x = 0 \) or \( x = 4 \).

So, the zeros of the function are \( x_1 = 0 \) and \( x_2 = 4 \).

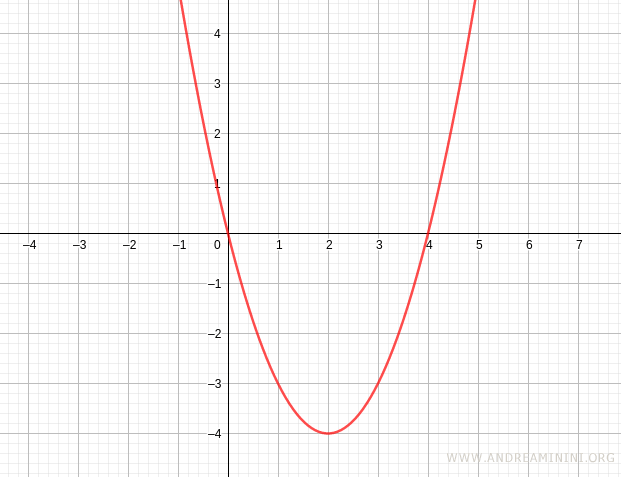
At \( x_1 = 0 \) and \( x_2 = 4 \), the graph of the function crosses the x-axis, since the function value is zero at those points.

And so on.