Polynomials

What are polynomials?

A polynomial is an algebraic expression made up of a sum of monomials.

Here’s a straightforward example of a polynomial:

$$ a^2c + bc + abc $$

This expression consists of the sum of three distinct monomials, which together form a polynomial.

What does "polynomial" mean? The term comes from the Greek “poly” (many) and the Latin “nomen” (term). So, a polynomial literally means “many terms.”

The monomials that make up a polynomial are called its terms.

Each term has a coefficient, which is the numerical factor in front of the variables.

For example, in the expression below, the polynomial has two terms. The coefficient of the first term is 3, while the second term has an implied coefficient of 1, which is not usually written explicitly in algebra:

$$ 3a + ab $$

If a polynomial includes a non-zero constant (a term with no variables), that term is referred to as the constant term.

For instance, in the following polynomial, the constant term is 3:

$$ 4a + 2ab + \color{red}3 $$

Depending on the number of terms, a polynomial in standard form is classified as follows:

• Monomial: one term
• Binomial: two terms
• Trinomial: three terms
• Quadrinomial: four terms

For example, the following is a binomial because it contains two terms:

$$ ab + 3bc $$

This next one is a trinomial since it contains three terms:

$$ ab + 3bc + c $$

When is a polynomial in standard form? A polynomial is in standard form when it contains only distinct monomials - in other words, no like terms. I’ll explain this in more detail in the next section, with a few practical examples.

Polynomials in standard form

A polynomial is in standard form (also called the simplified form) when all its terms are simplified and no like terms remain in the expression.

For instance, this is a polynomial in standard form because it contains no like terms:

$$ 3ab^2 + 5ab + c $$

By contrast, this one is not in standard form because it includes two like terms: 2ab and 3ab.

$$ 3ab^2 + 2ab + 3ab + c $$

How to write a polynomial in standard form

Any polynomial can be rewritten in standard form by combining like terms through algebraic addition.

Example

Let’s take this polynomial, which is not yet in standard form:

$$ 3ab^2 + 2ab + 3ab + c $$

Here, the terms 2ab and 3ab are like terms.

We combine them using the distributive property:

$$ 3ab^2 + (2+3) \cdot ab + c $$

$$ 3ab^2 + 5ab + c $$

The result is the same polynomial expressed in standard form.

Degree of a polynomial

The degree of a polynomial in standard form is the highest degree among its terms.

Example

In the following polynomial, the first term (a³b) has degree 4, while the second (ab²) and third (abc) each have degree 3:

$$ a^3b + ab^2 + abc $$

So, the polynomial is of degree 4.

Note: You should only determine the degree of a polynomial once it has been simplified to standard form. If it isn’t, simplify it first.

The degree of a polynomial with respect to a given variable is the highest exponent of that variable in the entire polynomial.

Example

This polynomial contains the variables a, b, and c:

$$ a^3b + ab^2 + abc + 5 $$

The degree with respect to "a" is 3, with respect to "b" is 2, and with respect to "c" is 1.

Constant term

The term in a polynomial with degree zero is called the constant term.

For instance, in this polynomial the constant term is 5:

$$ ab^3 + a^2bc + ab + 5 $$

Explanation: Any number not multiplied by a variable is considered to have degree zero. Since any variable raised to the power of zero equals one (e.g., a⁰ = 1), we can treat a number in a polynomial as the coefficient of a variable to the power of zero. For example: $$ 5 = 5 \cdot 1 = 5 \cdot a^0 $$ So, we can rewrite the polynomial $$ ab^3 + a^2bc + ab + 5 $$ as $$ ab^3 + a^2bc + ab + 5a^0 $$ These two forms are equivalent, confirming that the number 5 is indeed a term of degree zero.

Remarks and additional notes

Here are a few key facts about polynomials:

• Equal polynomials
  Two or more polynomials are considered equal if they contain the same terms, regardless of the order.

  Example: These two polynomials are equal: $$ 3ab + 2b + 4bc $$ $$ 2b + 4bc + 3ab $$ because they consist of the same monomials.

• The zero polynomial
  The number zero is known as the zero polynomial.

  Proof: Zero can be written as the product of the numerical coefficient zero and any variable. For example: $$ 0 = 0 \cdot a $$ Therefore, zero is also considered a monomial (specifically, a zero monomial). The sum of several zero monomials is still zero - hence, a zero polynomial. For example: $$ 0 \cdot a + 0 \cdot b = 0 $$ So, zero functions as both a zero monomial and a zero polynomial.

• Every monomial is a polynomial
  Any monomial can be regarded as a polynomial composed of itself and the zero monomial.

  For instance, this expression is a polynomial made of two distinct monomials: $$ 3ab + 0 $$ Thus, every monomial is, in fact, a polynomial in its own right: $$ 3ab + 0 = 3ab $$

• The set of polynomials includes both monomials and real numbers
  The set of monomials is a subset of the set of polynomials. Since the set of real numbers is itself a subset of the monomials, it too belongs to the broader set of polynomials. In other words, polynomials encompass not only monomials but also real numbers.
  

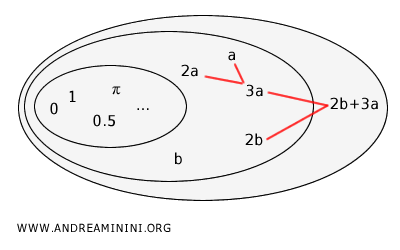
  Note. The set of monomials is not closed under addition, since the sum of two distinct monomials can result in a polynomial (e.g., \( 2b + 3a \)). However, adding a monomial to itself (e.g., \( a + a = 2a \)), or to the zero monomial (e.g., \( 2a + 0 = 2a \)), always yields another monomial. Therefore, every monomial is also a polynomial (e.g., \( 2a = 2a + 0 \): it qualifies as both a monomial and a polynomial), though the reverse does not hold: not every polynomial is a monomial (e.g., \( 2b + 3a \) is a polynomial, but not a monomial).

• The zero polynomial
  The zero polynomial is simply the number zero. It can be viewed either as a null monomial, \( 0 = 0 \cdot a^0 \), or as an algebraic sum of null monomials, \( 0 = 0 \cdot a^0 + 0 \cdot b^0 \).
• Homogeneous polynomial
  A polynomial is said to be homogeneous when all its terms share the same degree.

  For example, this polynomial is homogeneous because each term has degree 4: $$ ab^3 + a^2bc + b^3a $$

• Opposite polynomial
  The opposite of a polynomial P(x) is the polynomial - P(x), which contains the same terms with opposite signs.
  

  For example, given: $$ P(x): \ a^3 -2 a^2b + bc $$ the opposite polynomial is: $$ -P(x): \ -a^3 +2 a^2b - bc $$

• Ordered polynomial
  A polynomial is said to be ordered with respect to a variable if the exponents of that variable in its terms are arranged in either ascending or descending order.

  For example, this polynomial is ordered with respect to "a", but not with respect to "b": $$ 3a^4 + a^3b + a^2b^3 + 3b $$

• Complete polynomial
  A polynomial is said to be complete with respect to a variable if it includes all powers of that variable from the highest down to zero.

  For instance, this polynomial is complete with respect to "a": $$ a^3b + a^2b^3 + 3ab + 3 $$ Since the constant 3 can be rewritten as 3 = 3·1 = 3a⁰.

And so on.