Binomial expansion of (a+b)n

To expand the n-th power of a binomial \( (a + b)^n \), we use the general formula: $$ (a + b)^n = c_0a^n + c_1a^{n-1}b + c_2a^{n-2}b^2 + \ldots + c_{n-1}ab^{n-1} + c_nb^n $$ The coefficients \( c_0, c_1, c_2, \ldots, c_n \) correspond to the entries in the n-th row of Pascal’s Triangle.

How to Expand a Binomial Power

To compute \( (a + b)^n \), follow these steps:

First, write the powers of the first term, \( a \), in descending order from \( n \) to 0:

$$ a^n,\ a^{n-1},\ \ldots,\ a^1,\ a^0 $$

Then write the powers of the second term, \( b \), in ascending order from 0 to \( n \):

$$ b^0,\ b^1,\ \ldots,\ b^{n-1},\ b^n $$

Multiply each pair of powers at matching positions:

$$ a^nb^0,\ a^{n-1}b^1,\ \ldots,\ a^1b^{n-1},\ a^0b^n $$

Next, express the result as a sum of terms:

$$ a^nb^0 + a^{n-1}b^1 + \ldots + a^1b^{n-1} + a^0b^n $$

Since any nonzero number raised to the power of zero is 1, we simplify:

$$ a^n + a^{n-1}b + \ldots + ab^{n-1} + b^n $$

Now apply the appropriate coefficients from Pascal’s Triangle to each term:

$$ c_0a^n + c_1a^{n-1}b + \ldots + c_{n-1}ab^{n-1} + c_nb^n $$

These coefficients \( c_0, c_1, \ldots, c_n \) are taken directly from the n-th row of Pascal’s Triangle.

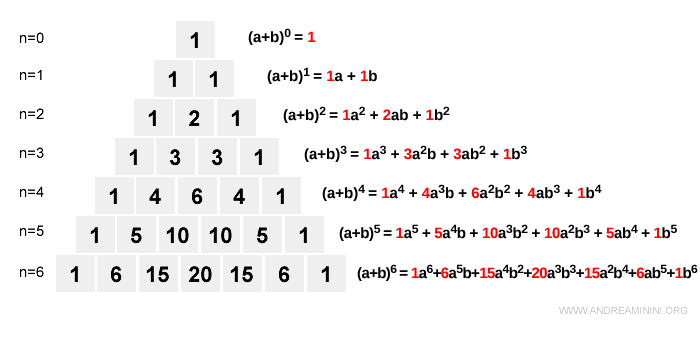
How is Pascal’s Triangle constructed? Begin with a triangle where the outer edges are all 1s. To complete each row, place in every inner position the sum of the two numbers directly above it from the previous row. This process is repeated indefinitely, building the triangle row by row.

For a detailed walkthrough, refer to the notes on Pascal’s Triangle.

The final result is the full expansion of the binomial raised to the n-th power.

Worked Example

Let’s expand the binomial \( (a + b)^4 \):

Start by writing the product of decreasing powers of \( a \) and increasing powers of \( b \):

$$ a^4b^0 + a^3b^1 + a^2b^2 + a^1b^3 + a^0b^4 $$

Simplify by omitting any term raised to the power of 0, and dropping the exponent 1:

$$ a^4 + a^3b + a^2b^2 + ab^3 + b^4 $$

Next, insert the binomial coefficients:

$$ c_0a^4 + c_1a^3b + c_2a^2b^2 + c_3ab^3 + c_4b^4 $$

From row 4 of Pascal’s Triangle, the coefficients are: \( c_0 = 1,\ c_1 = 4,\ c_2 = 6,\ c_3 = 4,\ c_4 = 1 \)

Substitute the values:

$$ 1 \cdot a^4 + 4 \cdot a^3b + 6 \cdot a^2b^2 + 4 \cdot ab^3 + 1 \cdot b^4 $$

Which simplifies to:

$$ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$

This is the full expansion of \( (a + b)^4 \).

Historical Notes

• The binomial expansion rule was developed in the 11th century by the Persian mathematician al-Karaji, who was able to compute powers of \( (a + b)^n \) up to \( n = 12 \).

And so on.