Cube of a Binomial
The cube of a binomial, (a + b)3, expands into a four-term expression known as a quadrinomial. It consists of the sum of the cubes of the two terms, plus three times the product of the square of the first term and the second, plus three times the product of the square of the second term and the first: $$ (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 $$
A Practical Example
Example 1
Let’s compute the cube of a binomial:
$$ (2a + 4b)^3 $$
Applying the formula directly:
$$ (2a + 4b)^3 = (2a)^3 + 3 \cdot (2a)^2 \cdot (4b) + 3 \cdot (2a) \cdot (4b)^2 + (4b)^3 $$
We simplify each term step by step:
$$ = 8a^3 + 3 \cdot 4a^2 \cdot 4b + 3 \cdot 2a \cdot 16b^2 + 64b^3 $$
$$ = 8a^3 + (3 \cdot 4 \cdot 4) \cdot a^2b + (3 \cdot 2 \cdot 16) \cdot ab^2 + 64b^3 $$
$$ = 8a^3 + 48a^2b + 96ab^2 + 64b^3 $$
Example 2
Now consider a binomial with a negative second term:
$$ (2a - 3b)^3 $$
Using the same approach:
$$ (2a - 3b)^3 = (2a)^3 + 3 \cdot (2a)^2 \cdot (-3b) + 3 \cdot (2a) \cdot (-3b)^2 + (-3b)^3 $$
Now simplify each component:
$$ = 8a^3 + 3 \cdot 4a^2 \cdot (-3b) + 3 \cdot 2a \cdot 9b^2 - 27b^3 $$
$$ = 8a^3 + (3 \cdot 4 \cdot -3) \cdot a^2b + (3 \cdot 2 \cdot 9) \cdot ab^2 - 27b^3 $$
$$ = 8a^3 - 36a^2b + 54ab^2 - 27b^3 $$
The Proof
To prove the formula, we start by observing that the cube of a binomial means multiplying it by itself three times:
$$ (a + b)^3 = (a + b) \cdot (a + b) \cdot (a + b) $$
This is equivalent to multiplying the binomial by its square:
$$ (a + b)^3 = (a + b)^2 \cdot (a + b) $$
The expansion of (a + b)^2 is already known (see proof):
$$ (a + b)^2 = a^2 + 2ab + b^2 $$
So the cube becomes:
$$ (a + b)^3 = (a^2 + 2ab + b^2) \cdot (a + b) $$
Now distribute each term:
$$ = (a^2 + 2ab + b^2) \cdot a + (a^2 + 2ab + b^2) \cdot b $$
$$ = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 $$
Combining like terms:
$$ = a^3 + (2a^2b + a^2b) + (ab^2 + 2ab^2) + b^3 $$
$$ = a^3 + 3a^2b + 3ab^2 + b^3 $$
This completes the derivation of the binomial cube formula.
Geometric Proof
Consider a cube with side length A+B.
Its volume is simply the cube of the side, so $ (A+B)^3 $.
Now, let’s break it down into 8 smaller components - 2 cubes and 6 rectangular prisms - and compute the volume of each one individually.
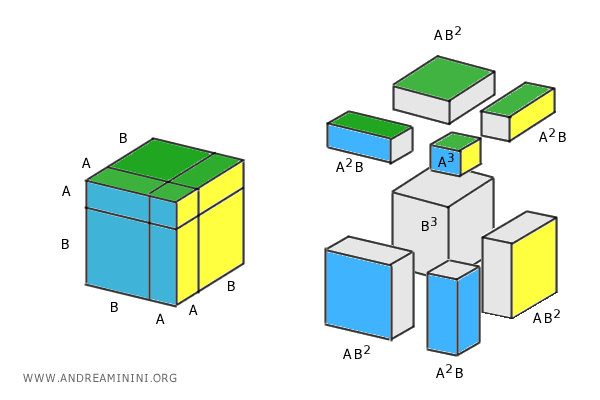
The total volume of the original cube is equal to the sum of the volumes of all these smaller parts.
$$ (A+B)^3 = A^3 + B^3 + AB^2 + AB^2 + AB^2 + A^2B + A^2B + A^2B $$
$$ (A+B)^3 = A^3 + B^3 + 3AB^2 + 3A^2B $$
This provides a clear geometric illustration of how the binomial cube formula comes together.
