Polynomial Division

What is polynomial division?

Dividing a polynomial A(x) by another polynomial B(x), written as $ A(x):B(x) $, means finding a quotient polynomial Q(x) such that: $$ A(x) = B(x) \cdot Q(x) + R $$ Here, A(x) is the dividend, B(x) is the divisor, Q(x) is the quotient, and R is the remainder.

If the remainder is zero (R = 0), then A(x) is exactly divisible by B(x).

$$ A(x):B(x) = \frac{A(x)}{B(x)} = Q(x) \quad \text{when } R = 0 $$

If the remainder is not zero, then A(x) is not divisible by B(x).

Note. Dividing two polynomials, A(x):B(x), always produces an algebraic fraction, but the result is not necessarily a polynomial. $$ A(x):B(x) = \frac{A(x)}{B(x)} $$ The result is a polynomial only if the division yields a quotient Q(x) with zero remainder (R = 0). For example, dividing x + 1 by x - 1 gives: $$ \frac{x+1}{x-1} $$ Since the remainder is not zero (R = 2), this expression is not a polynomial, though it is still an algebraic fraction.

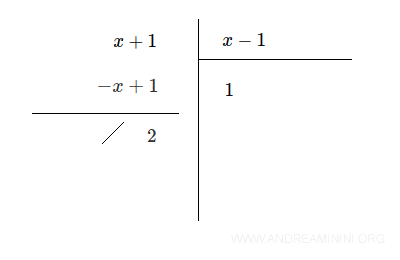
How to Divide Two Polynomials

To find the quotient Q(x), follow this algorithm step by step:

Set up the division as you would with numbers, writing the dividend P(x) and divisor Q(x) in long division format.

Note. If the degree of the divisor is greater than that of the dividend, the quotient is Q(x) = 0, and the division ends there.

Example: divide P(x) = x² + 5x + 7 by Q(x) = x + 3

Start by dividing the leading term of the dividend by the leading term of the divisor. Write this result as the first term of the quotient.

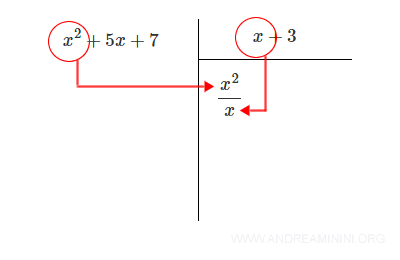
Here, the leading term of the dividend is x², and the leading term of the divisor is x. So the first term in the quotient is: x²/x = x

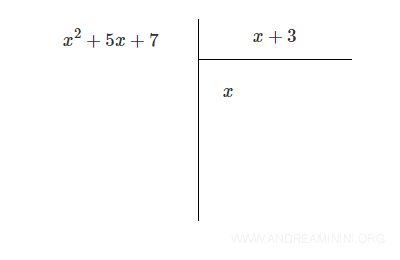
Next, multiply x by the entire divisor (x + 3): $$ x \cdot (x + 3) = x^2 + 3x $$

Now subtract this product from the dividend by writing it with opposite signs underneath: - (x² + 3x) = - x² - 3x

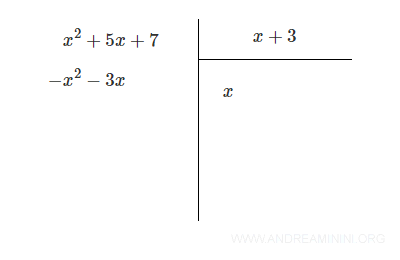
Draw a line and combine like terms: (x² + 5x + 7) + ( - x² - 3x)

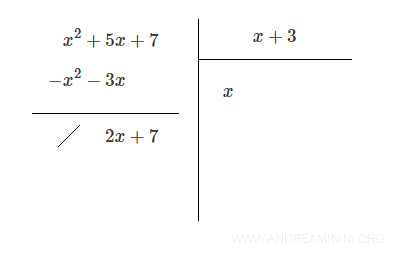
Repeat the process with the result.

Divide the new leading term (2x) by the leading term of the divisor (x): 2x / x = 2

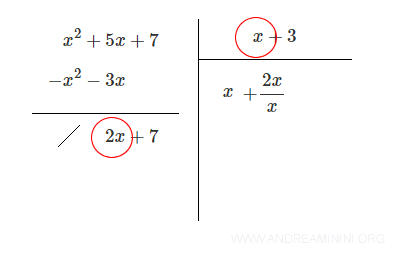
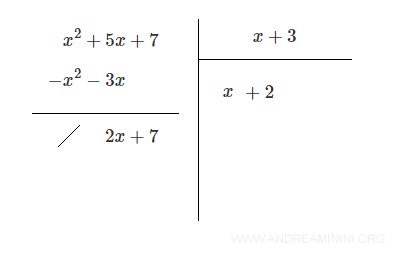
Multiply 2 by the divisor: $$ 2 \cdot (x + 3) = 2x + 6 $$

Then subtract: - (2x + 6) = - 2x - 6

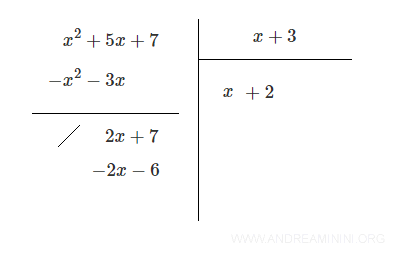
Finally, add the resulting polynomials: (2x + 7) + ( - 2x - 6) = 1

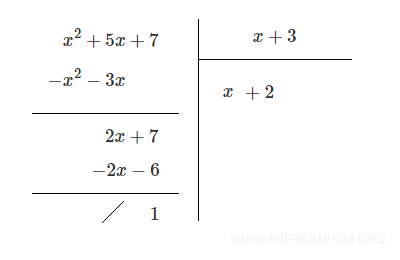
The remainder is 1, which has a lower degree than the divisor, so the division stops here.

Final result: Quotient Q(x) = x + 2 Remainder R = 1

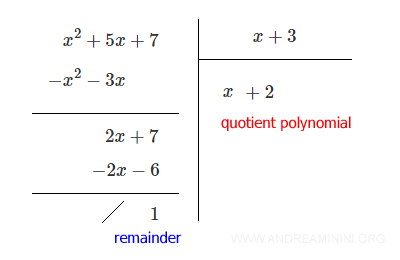
Since the remainder is not zero (R ≠ 0), the result is not a polynomial.

Verification. Let’s check the result: $$ Q(x) = x + 2 \quad R(x) = 1 $$ The dividend should satisfy: $$ A(x) = B(x) \cdot Q(x) + R(x) $$ Substitute B(x) = x + 3, Q(x) = x + 2, R(x) = 1: $$ A(x) = (x + 3)(x + 2) + 1 $$ Expanding: $$ A(x) = x^2 + 2x + 3x + 6 + 1 = x^2 + 5x + 7 $$ Which matches the original dividend A(x) = x² + 5x + 7, confirming the result is correct.

Example 2

Now divide A(x) = - 3x⁴ + 14x³ - 13x² + 2 by B(x) = 3x² - 2x - 1

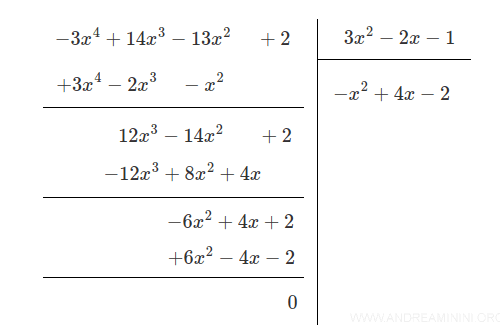
Result: The quotient is - x² + 4x - 2 and the remainder is R = 0.

Since the remainder is zero, the result is a polynomial.

Verification. Let’s verify the result: $$ Q(x) = -x^2 + 4x - 2 \quad R(x) = 0 $$ So, $$ A(x) = B(x) \cdot Q(x) + R(x) $$ Substitute: $$ A(x) = (3x^2 - 2x - 1)(-x^2 + 4x - 2) + 0 $$ Expand: $$ A(x) = -3x^4 + 2x^3 + x^2 + 12x^3 - 8x^2 - 4x - 6x^2 + 4x + 2 $$ $$ A(x) = -3x^4 + 14x^3 - 13x^2 + 2 $$ This matches the original dividend, so the division is correct.

Ruffini's Rule

Ruffini's rule is a shortcut method for dividing polynomials, but it only applies when the divisor is a binomial of the form x - k: $$ \frac{P(x)}{x - k} $$

This technique works only if the divisor is a binomial (x - k), where k is any real number.

Unlike polynomial long division, Ruffini's rule is not a general-purpose method - it applies only in this specific case.

Example

Let’s divide the polynomial P(x) = x² + 5x + 7 by Q(x) = x + 3:

$$ \frac{x^2 + 5x + 7}{x + 3} $$

The divisor is of the form (x - k) with k = - 3, so Ruffini’s rule can be used.

Start by writing the coefficients of the dividend across the top row. The constant term (7) comes after the second vertical line:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ & & & \\ \hline & & & \end{array} $$

Next, write the opposite of the constant term from the divisor to the left of the vertical bar. Since the constant in the divisor is 3, its opposite is - 3:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ \color{red}{-3}& & & \\ \hline & & & \end{array} $$

Bring down the first coefficient (1) directly to the bottom row:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & & \\ \hline &\color{red}{1} & & \end{array} $$

Multiply this value by - 3, and place the result in the second row, next column:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & \color{red}{-3 \cdot 1} & \\ \hline &1 & & \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & \color{red}{-3} & \\ \hline &1 & & \end{array} $$

Add the values in the second column: 5 + ( - 3) = 2, and write the result on the bottom row:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \\ \hline &1 & \color{red}{2} & \end{array} $$

Multiply this result (2) by - 3, and write it in the next column of the second row:

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \color{red}{-3 \cdot 2} \\ \hline &1 & 2 & \end{array} $$

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & \color{red}{-6} \\ \hline &1 & 2 & \end{array} $$

Now add the values in the final column: 7 + ( - 6) = 1

$$ \begin{array}{c|lc|r} & 1 & 5 & 7 \\ -3& & -3 & -6 \\ \hline &1 & 2 & \color{red}{1} \end{array} $$

The numbers between the vertical bars are the coefficients of the quotient polynomial, and the number to the right is the remainder.

Since the dividend x² + 5x + 7 is of degree 2 and the divisor x + 3 is degree 1, the quotient will be degree 1:

$$ Q(x) = x + 2 $$

$$ R = 1 $$

Note. The degree of the quotient is always one less than the degree of the dividend. In general, the degree of the quotient equals the degree of the dividend minus the degree of the divisor. Here, the dividend x² + 5x + 7 has degree 2, the divisor x + 3 has degree 1, so the quotient must have degree 1 (i.e., 2 - 1).

And so on.