Remainder Theorem

When dividing a polynomial by an expression of the form $$ \frac{P(x)}{x-k} = Q(x) + R $$ the remainder R is equal to the value of the polynomial P(x) evaluated at x = k: $$ P(k) = R $$ Here, k is the constant term from the divisor written in the form (x - k).

This is a fundamental property of polynomial division by a linear binomial of the form (x - k).

The theorem provides a shortcut for finding the remainder without having to carry out the full division.

Important: This result applies only when dividing by a binomial of the form (x - k). It does not hold for general polynomial division.

A practical example
Proof of the theorem

A practical example

Let’s consider the division of two polynomials:

$$ \frac{x^2 + 5x + 7}{x + 3} $$

We perform the division:

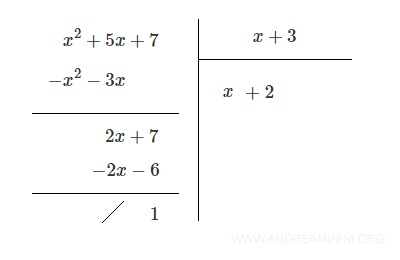
long division result: remainder is 1

The result is a quotient Q(x) = x + 2 with a remainder R = 1.

$$ \frac{x^2 + 5x + 7}{x + 3} = x + 2 \ \ \ \ \text{with remainder } R = 1 $$

According to the Remainder Theorem, the value of the polynomial evaluated at x = k should equal the remainder:

$$ P(k) = R \ \ \ \ \text{where } x = k $$

In this case, the divisor is (x + 1).

To apply the theorem properly, we rewrite it in the standard form (x - k):

$$ (x - (-1)) = (x + 1) $$

So here, k = -1.

Let’s evaluate the polynomial at x = -1:

$$ P(-1) = x^2 + 5x + 7 $$

$$ P(-1) = (-1)^2 + (-1) \cdot 5 + 7 $$

$$ P(-1) = 1 - 5 + 7 $$

$$ P(-1) = 3 $$

So, P(-1) = 3, which matches the remainder R = 3 from the division.

Proof of the theorem

The proof of the Remainder Theorem is straightforward.

Start with the division of a general polynomial P(x) by (x - k):

$$ \frac{P(x)}{x-k} = Q(x) \ \ \ \text{with remainder } R $$

Multiplying both sides of the equation by (x - k):

$$ \frac{P(x)}{x-k} \cdot (x - k) = Q(x) \cdot (x - k) \ \ \ \text{with remainder } R $$

Simplifying the left-hand side gives:

$$ P(x) = Q(x) \cdot (x - k) + R $$

Now substitute x = k into the equation:

$$ P(k) = Q(k) \cdot (k - k) + R $$

Since (k - k) = 0, the first term vanishes:

$$ P(k) = 0 + R $$

$$ P(k) = R $$

This confirms the validity of the Remainder Theorem.

And that's all there is to it.