Factoring Out the Common Term

What does it mean to factor out the common term?

Factoring out the common term is a factoring technique used to break down a polynomial P(x) of degree n into a product of lower-degree polynomials: $$ P_n(x) = A_s(x) \cdot B_t(x) $$ where s + t = n.

The sum of the degrees of the factors (s + t) equals the degree n of the original polynomial.

When a sum of terms shares a common factor, we can factor it out by placing it in front and multiplying it by the sum of the remaining parts.

$$ (xa + xb) = x \cdot (a + b) $$

Note. This result comes from applying the distributive property of multiplication over addition in reverse: x · (a + b) = x · a + x · b, and therefore, x · a + x · b = x · (a + b). $$ x \cdot a + x \cdot b = x \cdot (a + b) $$ Since multiplication is commutative, the distributive property applies both from the left and from the right: $$ x \cdot (a + b) = (a + b) \cdot x $$ So we can factor out the common term from either side: $$ x \cdot a + x \cdot b = x \cdot (a + b) = (a + b) \cdot x $$ The result remains the same either way.

A practical example

Example 1

Let’s consider a first-degree polynomial:

$$ 3a + 3b $$

Both terms share a common factor: 3.

We factor out the 3 and rewrite the expression as:

$$ 3 \cdot (a + b) $$

This is the result of factoring out the common term.

Note. You can factor from the left or the right: $$ 3a + 3b = 3 \cdot (a + b) = (a + b) \cdot 3 $$ The result is the same, thanks to the commutative property of multiplication.

Note 2. When the common factor is a numerical coefficient - as in this case - the factorization yields the product of a zero-degree polynomial and a polynomial of the same degree as the original. Here, n = 1. So even though one factor (the number 3) has degree 0, the total degrees still add up to 1: $$ \underbrace{3a + 3b}_{n=1} = \underbrace{3}_{0} \cdot \underbrace{(a + b)}_{1} = \underbrace{(a + b)}_{1} \cdot \underbrace{3}_{0} $$

Example 2

Every term in the following polynomial contains the factor x:

$$ 2x^3 - 5x^2 + x $$

We factor out x and rewrite the expression as:

$$ x \cdot (2x^2 - 5x + 1) $$

This gives us the product of a first-degree polynomial (x) and a second-degree polynomial (2x² - 5x + 1).

Note. The degrees of the factors - 1 and 2 - add up to the degree of the original polynomial: n = 3.

This factored form makes it much easier to solve the equation, since we can apply the zero-product property:

$$ x \cdot (2x^2 - 5x + 1) = 0 $$

If the first factor is zero (x = 0), the entire product is zero.

So x = 0 is a root of the equation 2x³ - 5x² + x = 0.

Note. A solution like x = 0 is referred to as a trivial solution.

To find the remaining solutions, we solve the quadratic equation from the second factor: 2x² - 5x + 1 = 0

We identify the coefficients: a = 2, b = -5, c = 1

$$ \Delta = b^2 - 4ac = (-5)^2 - 4(2)(1) = 25 - 8 = 17 $$

The discriminant is positive (Δ > 0), meaning the equation has two distinct real roots:

$$ x = \frac{-b \pm \sqrt{ \Delta }}{2a} $$

$$ x = \frac{-(-5) \pm \sqrt{17}}{2 \cdot 2} $$

$$ x = \frac{5 \pm \sqrt{17}}{4} $$

$$ x = \begin{cases} \frac{5 - \sqrt{17}}{4} \approx 0.22 \\ \\ \frac{5 + \sqrt{17}}{4} \approx 2.28 \end{cases} $$

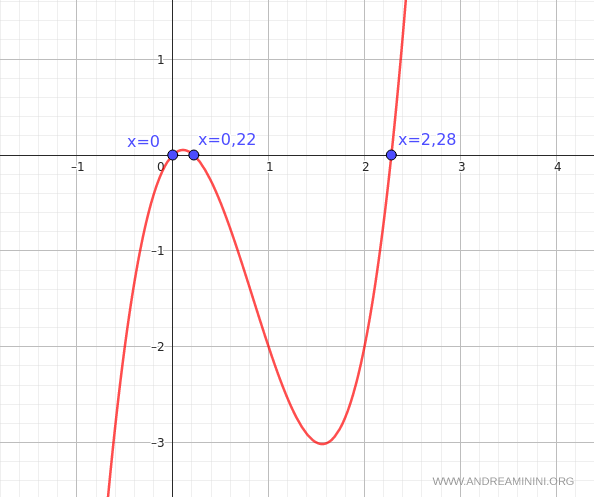
So, the original polynomial 2x³ - 5x² + x has three distinct solutions:

$$ x_1 = 0 $$

$$ x_2 \approx 0.22 $$

$$ x_3 \approx 2.28 $$

We’ve now found all the roots of the cubic equation 2x³ - 5x² + x = 0.

Verification. To verify the results, we can graph the polynomial. The graph of P(x) crosses the x-axis at x = 0, x ≈ 0.22, and x ≈ 2.28, confirming these are indeed the roots.

And so on.