Pascal’s Triangle

Pascal’s Triangle is a geometric arrangement of the binomial coefficients that appear in the expansion of $ (a + b)^n $.
Pascal’s Triangle from row 0 to row 7

These coefficients correspond to the terms in the polynomial resulting from the binomial expansion of $ (a + b)^n $.

Pascal’s Triangle is also referred to in Italian as the “Triangolo di Tartaglia.”

How to Build Pascal’s Triangle
Combinations and Pascal’s Triangle

How to Build Pascal’s Triangle

The triangle begins with the number 1 at the top - this forms the zeroth row, denoted by $ n = 0 $:

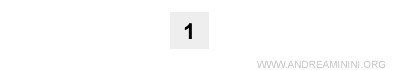
The number 1 at the apex of the triangle

Each subsequent number is obtained by summing the two adjacent numbers directly above it in the previous row. Blank spaces are treated as zeros.

Following this rule, we construct the first row (n = 1):

First row after the apex

Note. The entries in row one (n = 1) represent the coefficients of the expansion: $$ (a + b)^1 = a + b $$ Here, both terms have coefficients equal to 1.

We apply the same method to generate the second row (n = 2):

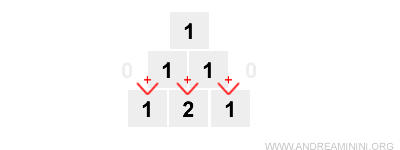
Second row of Pascal’s Triangle

Note. The coefficients in row two (n = 2) correspond to the expansion: $$ (a + b)^2 = a^2 + 2ab + b^2 $$ That is: 1$ a^2 $ + 2$ ab $ + 1$ b^2 $

Next, we continue with the third row (n = 3):

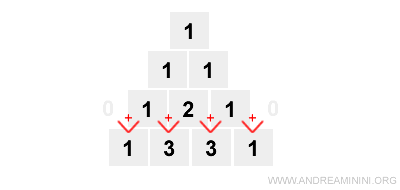
Expansion of (a + b)^3

Note. Row three (n = 3) provides the coefficients for: $$ (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 $$ That is: 1$ a^3 $ + 3$ a^2b $ + 3$ ab^2 $ + 1$ b^3 $

Then we construct the fourth row (n = 4):

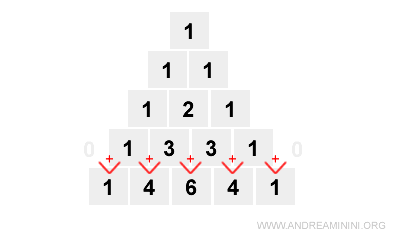
Fourth row of the triangle

Note. Row four (n = 4) corresponds to: $$ (a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$ In terms of coefficients: 1$ a^4 $ + 4$ a^3b $ + 6$ a^2b^2 $ + 4$ ab^3 $ + 1$ b^4 $

This same process can be used to generate any row of Pascal’s Triangle for higher values of $ n $.

In theory, the triangle extends infinitely downward.

Pascal’s Triangle up to row 7

Combinations and Pascal’s Triangle

Each entry in Pascal’s Triangle also represents a binomial coefficient, or combination, denoted $$ C(n, k) = \begin{pmatrix} n \\ k \end{pmatrix} $$ where $ n $ is the row number and $ k $ is the element’s position within the row.

Note. Both $ n $ and $ k $ start at 0. So the top row is $ n = 0 $, and the first position in each row is $ k = 0 $, and so on.

Example

The number 10 appears in row $ n = 5 $, at position $ k = 2 $:

Pascal’s Triangle and combinations

To confirm this, we compute the combination:

$$ \begin{pmatrix} 5 \\ 2 \end{pmatrix} = \frac{5!}{2!(5 - 2)!} = \frac{120}{12} = 10 $$

This means there are 10 ways to choose 2 elements from a set of 5 - exactly matching the value found in the triangle.

This illustrates the direct correspondence between the entries in Pascal’s Triangle and binomial coefficients.

And so on.