Operations with Polynomials
The fundamental mathematical operations involving two polynomials.
Adding Polynomials
The sum of two polynomials is another polynomial formed by combining all like terms and simplifying to standard form.
Example. Consider the polynomials: $$ P(x): \ 2x^2 + 3x + 2 \quad\quad Q(x): \ 4x^2 + 5x + 6 $$ To find their sum, we add all corresponding terms: $$ P(x) + Q(x) = (2x^2 + 3x + 2) + (4x^2 + 5x + 6) $$ Now simplify: $$ P(x) + Q(x) = 2x^2 + 3x + 2 + 4x^2 + 5x + 6 $$ $$ P(x) + Q(x) = x^2(2 + 4) + x(3 + 5) + (2 + 6) $$ $$ P(x) + Q(x) = 6x^2 + 8x + 8 $$
Subtracting Polynomials
To subtract one polynomial from another, you add the opposite (i.e., the additive inverse) of the second polynomial to the first. See opposite polynomial for more details.
Example. Consider: $$ P(x): \ 2x^2 + 3x + 2 \quad\quad Q(x): \ 4x^2 + 5x + 6 $$ To compute \( P(x) - Q(x) \), we add the opposite of \( Q(x) \): $$ P(x) - Q(x) = (2x^2 + 3x + 2) + (-4x^2 - 5x - 6) $$ Then simplify: $$ P(x) - Q(x) = 2x^2 + 3x + 2 - 4x^2 - 5x - 6 $$ $$ P(x) - Q(x) = x^2(2 - 4) + x(3 - 5) + (2 - 6) $$ $$ P(x) - Q(x) = -2x^2 - 2x - 4 $$
Multiplying Polynomials
To multiply two polynomials, use the distributive property: multiply each term in the first polynomial by each term in the second, then combine like terms.
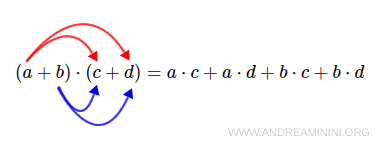
The degree of the resulting polynomial is the sum of the degrees of the two factors.
Example. Multiply the following polynomials: $$ (2a + 3b)(3a - 4b) $$ Apply the distributive property: $$ 2a(3a - 4b) + 3b(3a - 4b) $$ $$ = 6a^2 - 8ab + 9ab - 12b^2 $$ Now simplify: $$ = 6a^2 + ab - 12b^2 $$ The product is a second-degree polynomial, as expected - the degree equals the sum of the degrees of the original polynomials.
In special cases, you can use notable identities to simplify multiplication without fully expanding the terms.
Here are a few common examples:
- Product of a sum and difference $$ (a + b)(a - b) = a^2 - b^2 $$
- Square of a binomial $$ (a + b)^2 = a^2 + 2ab + b^2 $$
- Square of a trinomial $$ (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc $$
- Square of a four-term polynomial $$ (a + b + c + d)^2 = a^2 + b^2 + c^2 + d^2 + \\ + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd $$
- Cube of a binomial $$ (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 $$
Dividing Polynomials
A polynomial \( A \) (the dividend) can be divided by a non-zero monomial or polynomial \( B \) (the divisor) if and only if there exists a quotient polynomial \( Q \) such that: $$ A : B = Q \quad \Leftrightarrow \quad B \cdot Q + R = A $$ where \( R \) is the remainder polynomial, which may be zero.
Division is only possible if the degree of the dividend is greater than or equal to that of the divisor.
The degree of the quotient is equal to the difference between the degrees of the dividend and the divisor.
Example. Consider the polynomials: $$ P(x): \ x^2 + 5x + 7 \quad\quad Q(x): \ x + 3 $$ In this case, the division yields a quotient polynomial: $$ Q(x): \ x + 2 $$ There’s a straightforward procedure for performing polynomial division, which I’ve explained in detail in another note (how to divide polynomials).

The quotient \( Q(x) \) is a first-degree polynomial. This matches the difference between the degrees of the dividend (2) and the divisor (1).
And so on.
