Product of Two Polynomials

The product of two polynomials, P and Q, is another polynomial obtained by multiplying each term of the first polynomial, P, by each term of the second polynomial, Q, and then summing all the resulting terms.

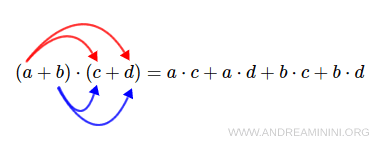
The degree of the resulting polynomial is equal to the sum of the degrees of the two original polynomials.

How many terms does the product of two polynomials have?

If the first polynomial has $m$ terms and the second has $n$ terms, their product will initially have $m \cdot n$ terms, before combining any like terms. After simplifying by combining like terms (for instance, $a + 2a = 3a$), the number of terms may be reduced.

This guideline is a handy way to check that no terms have been missed during multiplication.

Example. Consider the product of two first-degree polynomials: $$ (2a + 3b) \cdot (3a - 4b) $$ Applying the associative and distributive properties, we expand as follows: $$ 2a \cdot (3a - 4b) + 3b \cdot (3a - 4b) $$ As expected, the expanded form has four terms: $$ 6a^2 - 8ab + 9ab - 12b^2 $$ We then combine like terms to simplify the expression: $$ 6a^2 + ab - 12b^2 $$ The final result is a second-degree polynomial consisting of three terms.

When multiplying a monomial by a polynomial, we simply apply the distributive property.

To multiply a monomial by a polynomial, multiply the monomial by each term of the polynomial individually, and then add the results.

$$ a \cdot (a+b+c) = a \cdot a + a \cdot b + a \cdot c = a^2 + ab + ac $$

Since multiplication is commutative, it makes no difference whether the monomial comes first or second - the result will be the same.

Example. Consider the product of a polynomial and a monomial: $$ (2a + 3b) \cdot 3c $$ Once again, we distribute the monomial across each term of the polynomial: $$ 2a \cdot 3c + 3b \cdot 3c = 6ac + 9bc $$ The final result is another first-degree polynomial.

Proof

This algebraic rule can also be illustrated using basic geometric reasoning.

Imagine a rectangle with a base measuring (a + b) and a height of (c + d).

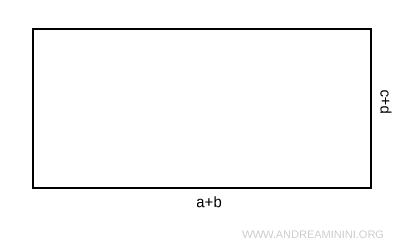
The area A of the rectangle is equal to the product of its base and height:

$$ A = (a+b) \cdot (c+d) $$

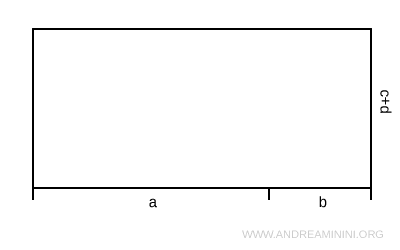
Now, divide the base into two segments: a and b.

Then, divide the height into two segments: c and d.

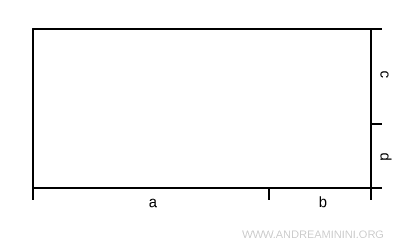
This subdivision creates four smaller, non-overlapping rectangles whose combined area equals the area of the original rectangle.

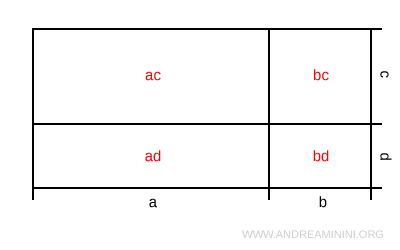
Therefore, the total area A can be expressed as the sum of the areas of the four smaller rectangles:

$$ A = ac + ad + bc + bd $$

In conclusion, the area of the rectangle can be written as:

$$ A = (a+b) \cdot (c+d) = ac + ad + bc + bd $$

This provides a clear geometric demonstration of how the distributive property works when multiplying two polynomials.

And so on.