Squaring a Binomial

The square of a binomial, (a + b)², is a trinomial obtained by summing the square of the first term (a²), the square of the second term (b²), and twice the product of the two terms (2ab). $$ (a + b)^2 = a^2 + b^2 + 2ab $$

This is a general formula that also applies when one or both terms are negative.

When calculating the double product (2ab), just remember to follow the sign rule.

Note. According to the rules of signs in algebra, the product of two terms with the same sign is always positive. If the signs differ, the product is negative.

A Practical Example

Example 1

Let’s start with a simple binomial:

$$ (3a + 2b)^2 $$

To expand it, we square each term and add twice their product:

$$ (3a)^2 + (2b)^2 + 2 \cdot (3a) \cdot (2b) $$

Now we apply the associative and commutative properties of multiplication to simplify:

$$ 9a^2 + 4b^2 + (2 \cdot 3 \cdot 2) \cdot (a \cdot b) $$

Which gives us the expanded form:

$$ 9a^2 + 4b^2 + 12ab $$

Example 2

Now let’s look at a case where the second term is negative:

$$ (3a - 2b)^2 $$

We apply the same binomial square rule:

$$ (3a)^2 + (-2b)^2 + 2 \cdot (3a) \cdot (-2b) $$

Squares are always positive, since each is the product of a term by itself.

The double product, however, is negative because the terms have opposite signs:

$$ 9a^2 + 4b^2 + [2 \cdot 3 \cdot (-2)] \cdot (a \cdot b) $$

So the final expanded form is:

$$ 9a^2 + 4b^2 - 12ab $$

Here, the double product is negative.

Example 3

Lastly, let’s consider when both terms are negative:

$$ (-3a - 2b)^2 $$

Again, we use the binomial square formula:

$$ (-3a)^2 + (-2b)^2 + 2 \cdot (-3a) \cdot (-2b) $$

$$ 9a^2 + 4b^2 + [2 \cdot (-3) \cdot (-2)] \cdot (a \cdot b) $$

The squares are positive, and this time the double product is also positive, because the two terms have the same (negative) sign.

$$ 9a^2 + 4b^2 + 12ab $$

This is the expanded form of the squared binomial.

The Geometric Proof

There’s also a geometric way to prove the binomial square formula.

Start with two line segments, a and b, of different lengths.

When we place them end to end, we get a new segment of length (a + b).

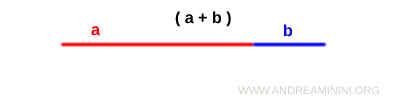
Now, construct a square on that segment, using (a + b) as the side length.

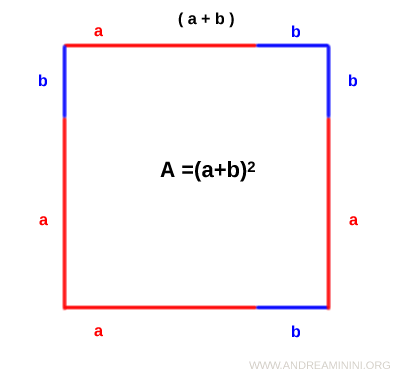
The area of the square is given by side times side: (a + b)·(a + b), or (a + b)².

$$ A = (a + b) \cdot (a + b) = (a + b)^2 $$

The ancient Greeks observed that this square could be broken down into two smaller squares and two identical rectangles, arranged neatly without overlap.

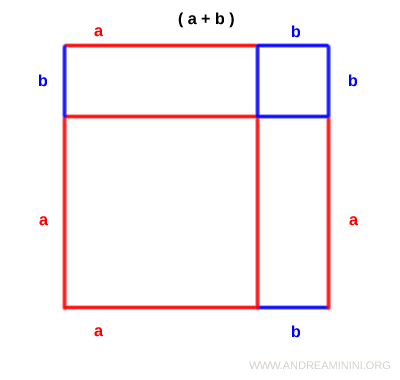
Let’s calculate the areas of these smaller regions.

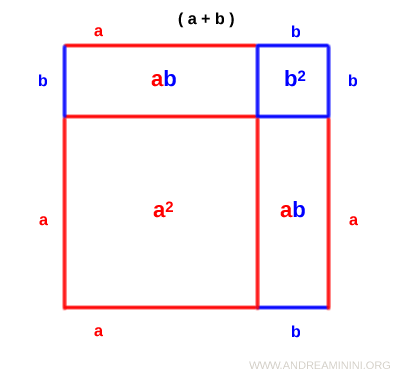
The total area of the two squares and two rectangles - namely a², b², ab, and ab - is exactly equal to the area of the large square:

$$ A = (a + b)^2 = a^2 + b^2 + ab + ab $$

By combining the two identical terms ab, we arrive at the standard formula for squaring a binomial:

$$ A = (a + b)^2 = a^2 + b^2 + 2ab $$

This geometric proof dates back over two thousand years, yet it remains one of the most intuitive and elegant ways to understand the binomial square rule.

And so on.