Product of the Sum and Difference of Two Monomials
The product of the sum and difference of two monomials is equal to the difference between the square of the first monomial and the square of the second. $$ (a+b) \cdot (a-b) = a^2 - b^2 $$
A Practical Example
Let’s take two polynomials, P(x) and Q(x), built from the sum and the difference of the monomials 4a and 2b.
$$ P(x): \ 4a + 2b $$
$$ Q(x): \ 4a - 2b $$
We want to compute the product of these two polynomials:
$$ P(x) \cdot Q(x) = (4a+2b) \cdot (4a-2b) $$
To solve this, we apply the identity known as the difference of squares:
$$ P(x) \cdot Q(x) = (4a)^2 - (2b)^2 $$
Therefore, the result of this special product is:
$$ P(x) \cdot Q(x) = 16a^2 - 4b^2 $$
Proof
We can demonstrate this identity using a geometric approach.
Imagine two line segments of lengths a and b.
Now, draw a rectangle where the base measures (a + b) and the height measures (a - b).
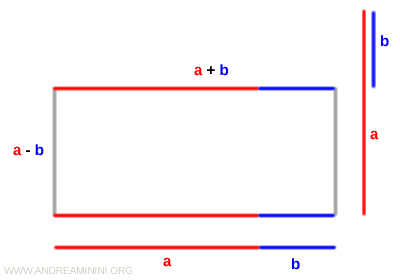
The area of this rectangle is given by:
$$ \text{Area} = (a + b) \cdot (a - b) $$
Let’s divide the rectangle into two smaller rectangles of equal height (a - b).
One has a base of length a, and the other has a base of length b.
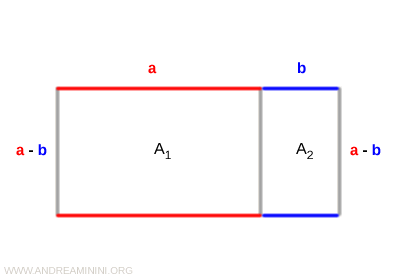
The total area A of the original rectangle is the sum of the areas A1 and A2 of the two smaller rectangles:
$$ A = A_1 + A_2 $$
We calculate the individual areas as follows:
$$ A_1 = a \cdot (a - b) = a^2 - ab $$
$$ A_2 = b \cdot (a - b) = ab - b^2 $$
Adding them together, we get:
$$ A = (a^2 - ab) + (ab - b^2) $$
$$ A = a^2 - ab + ab - b^2 $$
The middle terms cancel each other out, leaving us with:
$$ A = a^2 - b^2 $$
This geometric proof confirms the identity for the product of the sum and difference of two terms.
And so on.
