Maclaurin Series for the Cosine Function

The Maclaurin series expansion for the cosine function is: $$ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + \frac{(-1)^n x^{2n}}{(2n)!} + o(x^{2n}) $$

Proof

Consider the Maclaurin series formula:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$

Here, the function is f(x) = cos(x).

For k = 0

Since f⁽⁰⁾(x) = f(x) = cos(x):

$$ \frac{f^{(0)}(0)}{0!} \cdot x^0 = \frac{\cos(0)}{0!} \cdot x^0 = \frac{1}{1} \cdot 1 = 1 $$

Therefore, the first term of the Maclaurin series is 1:

$$ \cos(x) = 1 + o(x^0) $$

$$ \cos(x) = 1 + o(1) $$

For k = 1

The first derivative of cos(x) is -sin(x):

$$ \frac{f^{(1)}(0)}{1!} \cdot x^1 = \frac{D[\cos(0)]}{1!} \cdot x = \frac{-\sin(0)}{1} \cdot x = 0 $$

So, the first-order term in the Maclaurin series is zero:

$$ \cos(x) = 1 + 0 + o(x^1) $$

For k = 2

The second derivative of cos(x) is -cos(x):

$$ \frac{f^{(2)}(0)}{2!} \cdot x^2 = \frac{D^{(2)}\cos(0)}{2!} \cdot x^2 = \frac{-\cos(0)}{2!} \cdot x^2 = -\frac{x^2}{2} $$

Therefore, the second-order term in the Maclaurin series is:

$$ \cos(x) = 1 + 0 - \frac{x^2}{2} + o(x^2) $$

For k = 3

The third derivative of cos(x) is sin(x):

$$ \frac{f^{(3)}(0)}{3!} \cdot x^3 = \frac{D^{(3)}\cos(0)}{3!} \cdot x^3 = \frac{\sin(0)}{3!} \cdot x^3 = 0 $$

Hence, the third-order term in the series is zero:

$$ \cos(x) = 1 + 0 - \frac{x^2}{2} + 0 + o(x^3) $$

For k = 4

The fourth derivative of cos(x) is cos(x) itself:

$$ \frac{f^{(4)}(0)}{4!} \cdot x^4 = \frac{D^{(4)}\cos(0)}{4!} \cdot x^4 = \frac{\cos(0)}{4!} \cdot x^4 = \frac{x^4}{4!} $$

Thus, the fourth-order term in the Maclaurin series is:

$$ \cos(x) = 1 + 0 - \frac{x^2}{2} + 0 + \frac{x^4}{4!} + o(x^4) $$

For k = 5

The fifth derivative of cos(x) is -sin(x):

$$ \frac{f^{(5)}(0)}{5!} \cdot x^5 = \frac{D^{(5)}\cos(0)}{5!} \cdot x^5 = \frac{-\sin(0)}{5!} \cdot x^5 = 0 $$

So the fifth-order term in the series is zero:

$$ \cos(x) = 1 + 0 - \frac{x^2}{2} + 0 + \frac{x^4}{4!} + 0 + o(x^5) $$

In summary, the Maclaurin series for cos(x) up to the fifth-order term is:

$$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^5) $$

Graphically, it appears as follows:

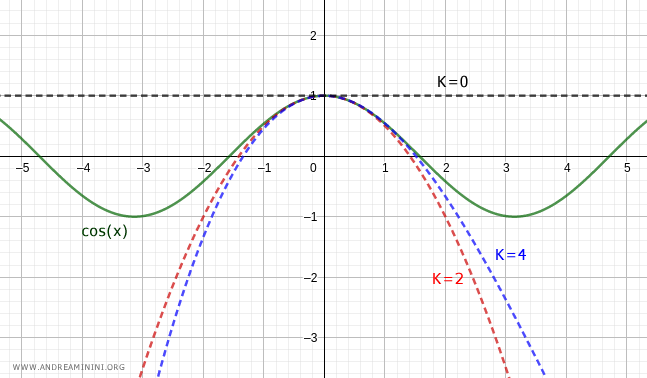
Note. Notice how the terms in the series alternate between nonzero and zero values. Consequently, the Maclaurin series for cos(x) up to order 4: $$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^4) $$ and up to order 5: $$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^5) $$ are essentially identical, differing only in the order of the little-o term at the end.

And so on.