Mathematical Logic
What Is Mathematical Logic?
Mathematical logic is a branch of mathematics that employs formal logical tools to analyze and establish the foundations of mathematical reasoning.
Bridging the fields of mathematics, logic, and philosophy, mathematical logic focuses on the study of formal structures, proofs, axioms, and mathematical models. Its primary aim is to ensure rigor, precision, and consistency in mathematical reasoning.
In essence, it is the study of reasoning itself, conducted through the framework of mathematical methodology.
What is the mathematical method? The mathematical method involves deriving propositions from definitions and axioms. It formalizes logical reasoning by expressing it in a structured, calculable form.
For this reason, mathematical logic is also referred to as formal logic or symbolic logic.
At its core, mathematical logic revolves around logical propositions.
Fundamental Tools of Mathematical Logic
Mathematical logic relies on a rigorous symbolic language designed to eliminate ambiguity and enhance precision.
Key components include:
- Logical connectives: Operators such as "and" (∧), "or" (∨), "not" (¬), and "if... then..." (→) that enable the formulation of complex logical statements.
- Quantifiers: The universal quantifier (∀) and the existential quantifier (∃) allow statements to be made about entire sets or individual elements that satisfy specific properties.
- Axioms and inference rules: These define the fundamental assumptions of a formal system and provide the mechanisms for deriving new theorems.
A logical proposition is a statement that is either true or false.
For example, consider this logical proposition:

This proposition can be rewritten in mathematical form as (A = B).
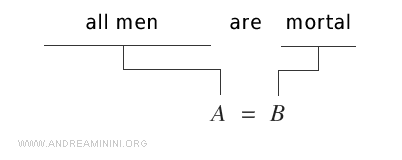
The fundamental meaning remains unchanged—whether expressed in natural language or in symbolic notation.
Each proposition is assigned a truth value (true or false).
Note: Multiple propositions can be linked through deductive reasoning.
Once a logical proposition has been formalized mathematically, it can be manipulated using logical operations such as negation, conjunction, and disjunction.
- Negation (¬)
Reverses the truth value of a proposition. If a proposition is true, its negation is false, and vice versa. - Conjunction (∧)
Combines two propositions, requiring both to be true for the overall expression to be true. If either proposition is false, the conjunction is false. - Disjunction (∨)
Links two propositions, asserting that at least one must be true for the overall statement to be true. If both are false, the disjunction is false.
Moreover, quantifiers extend logical reasoning to broader mathematical domains.
- Universal quantifier (∀)
States that a given property holds for all elements of a set. - Existential quantifier (∃)
Asserts the existence of at least one element that satisfies a given condition.
The systematic application of these logical operations and symbolic expressions enables the construction of formal proofs, ensuring that each step in a logical argument is rigorously justified and follows from axioms or previously established theorems.
Note: These tools make it possible to construct intricate logical frameworks and verify the validity of entire sequences of propositions. Fundamental principles such as the law of the excluded middle and the principle of non-contradiction play a crucial role in this process. Additionally, techniques such as natural deduction and predicate calculus provide powerful methods for assessing the logical consistency and validity of mathematical arguments, ensuring that conclusions are soundly derived from well-founded premises.
Origins of Mathematical Logic
Mathematical logic has its roots in ancient philosophy, tracing back to Aristotelian logic. However, it was only in the 19th and 20th centuries that it developed into a formal mathematical discipline, thanks to the foundational work of George Boole, Gottlob Frege, Bertrand Russell, and David Hilbert.
These pioneers sought to establish a rigorous framework for mathematics, employing a formal symbolic language to eliminate ambiguity and inconsistencies.
Frege was particularly instrumental in this transformation, introducing the first fully developed system of formal logic in his seminal work Begriffsschrift (1879).
Later, Hilbert advanced the axiomatic method, advocating for a systematic foundation of mathematics based on well-defined principles. Meanwhile, Russell, in collaboration with Alfred North Whitehead, authored the monumental Principia Mathematica, an ambitious attempt to derive all of mathematics from logical principles.
Distinguishing Logic from Mathematical Logic. Logic, in its broadest sense, is the study of reasoning and argumentation. It seeks to analyze the principles of valid inference and rational thought. The discipline originated in ancient Greece, where Aristotle laid the groundwork for classical logic. However, in antiquity, logic was primarily a philosophical pursuit, developed through dialectical reasoning rather than through formal scientific methods, which had yet to emerge.
Mathematical logic, by contrast, is a modern refinement of this tradition. It arose when logical reasoning was formalized using mathematical structures, allowing for precise manipulation and analysis. In mathematical logic, mathematics serves both as a tool and as an object of study: it provides the formal apparatus for investigating logical systems while simultaneously being subjected to logical scrutiny itself.
Major Branches and Theories in Mathematical Logic
Mathematical logic is divided into several key areas, each addressing fundamental aspects of logical and mathematical structure:
- Set Theory
The study of sets—collections of mathematical objects—serves as the foundation for much of modern mathematics. Set theory provides the framework for defining numbers, functions, and various mathematical structures. It also addresses paradoxes such as Russell's paradox, which revealed foundational challenges in the naive conception of sets. - Model Theory
Investigates the relationship between formal languages—symbolic systems used to articulate mathematical theories—and the mathematical structures they describe. Model theory explores the extent to which an axiomatic system can be interpreted across different models, analyzing equivalences, distinctions, and limitations in formal representations. - Computability Theory
Examines the boundaries of algorithmic computation, distinguishing between problems that can be solved by systematic procedures and those that cannot. This field introduced foundational concepts such as Turing machines (conceived by Alan Turing), theoretical models of computation that formalize the notion of algorithmic processes. Computability theory is closely linked to complexity theory, which investigates the computational resources—such as time and space—required to solve different classes of problems. - Proof Theory
Studies the structure, nature, and limitations of mathematical proofs. It seeks to formalize the notion of proof itself, ensuring that derivations within a logical system are sound and rigorous. A cornerstone of this field is Gödel's incompleteness theorems, which demonstrated that in any sufficiently expressive formal system, there exist true statements that cannot be proven within the system’s own framework.
These fields collectively provide the foundation for a formal, rigorous understanding of logic and its applications in mathematics.
