Vector Subspaces and Linear Combinations

Let V be a vector space over a field K, and let W be a subset of V. We say that W is a vector subspace of V if it is closed under linear combinations.

In other words, for any

$$ w_1, ..., w_m \in W \quad \text{and} \quad a_1, ..., a_m \in K $$

the following holds:

$$ a_1 w_1 + \dots + a_m w_m \in W $$

Explanation

The requirement that linear combinations of elements in W remain in W encapsulates the two fundamental properties that define a vector subspace:

1. For any $w_1, w_2 \in W$, their sum $w_1 + w_2$ also belongs to W.
   
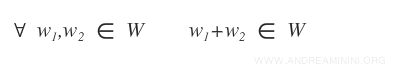
2. For any scalar $\lambda \in K$ and any $w \in W$, the product $\lambda w$ also belongs to W.
   

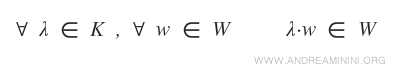
As a result, any linear combination of vectors in W is still an element of the larger vector space V.

Thus, W qualifies as a vector subspace of V.

The Set L_k of All Linear Combinations

Given vectors $v_1, \dots, v_m$ in a vector space V over a field K, the set of all linear combinations of these vectors with coefficients from K is denoted by $L_k$:
$$ L_k \{ v_1, \dots, v_m \} = \left\{ \alpha_1 v_1 + \dots + \alpha_m v_m \mid \alpha_1, \dots, \alpha_m \in K \right\} $$

The set $L_k$ is a vector subspace of V because it is closed under both vector addition and scalar multiplication - hence under linear combinations in general.

It is also the smallest vector subspace of V that contains the vectors $v_1, \dots, v_m$.

Note. In linear algebra textbooks, the set $L_k$ is sometimes denoted using alternative notations, such as Link or span_K.