Networkx Module for Graphs in Python

To work with graphs in Python, you can use the networkx module. This module is specifically designed for handling both simple and multi-graphs, as well as directed graphs (digraphs).

First, you need to install it on your PC using the pip command, as it’s not included in Python’s standard library.

pip install networkx

Once installed, you can import it into your code and start using all the functions available in the library.

An Example of a Simple Graph

To visualize the graph, you'll also need to import the matplotlib library.

import networkx as nx
import matplotlib.pyplot as plt

This allows you to define a graph and assign it to the variable G using the Graph() method.

G = nx.Graph()

Then, add edges between the nodes of the graph using the add_edge() method.

G.add_edge('A', 'B')
G.add_edge('B', 'C')
G.add_edge('C', 'A')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('B', 'E')
G.add_edge('D', 'E')

For example, add_edge('A', 'B') adds a connection between nodes 'A' and 'B', while add_edge('B', 'C') connects nodes 'B' and 'C'.

In this example, you don't need to define the nodes separately; just add the connections and the nodes are automatically included in the graph.

Once the graph is complete, you can draw it using the draw() method.

nx.draw(G, with_labels=True)
plt.show()

The result looks like this:

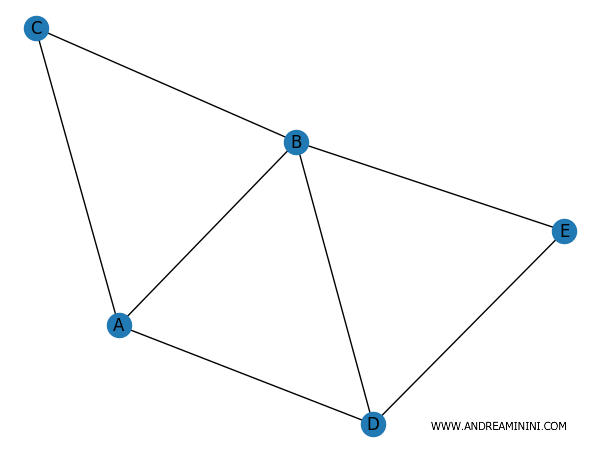
The networkx module isn't just useful for visualizing graphs, which is a basic feature, but it also allows you to analyze the key characteristics of the graph.

For example, you can calculate the degree of each node using the degree() method.

The degree of a node is the number of connections it has. For instance, node A has 3 edges, while node C has only 2.

degrees = dict(G.degree())
print(degrees)

{'A': 3, 'B': 4, 'C': 2, 'D': 3, 'E': 2}

You can also find the connected components of the graph.

components = list(nx.connected_components(G))
print(components)

[{'C', 'D', 'A', 'B', 'E'}]

Or find the shortest path between two nodes. For example, between nodes A and E. One of the shortest paths is A→B→E.

shortest_path = nx.shortest_path(G, source='A', target='E')
print(shortest_path)

['A', 'B', 'E']

You can also calculate the betweenness centrality of the nodes.

centrality = nx.betweenness_centrality(G)
print(centrality)

{'A': 0.08333333333333333, 'B': 0.3333333333333333, 'C': 0.0, 'D': 0.08333333333333333, 'E': 0.0}

Additionally, you can compute the minimum spanning tree of the graph.

T = nx.minimum_spanning_tree(G)
print(T)

Graph with 5 nodes and 4 edges

An Example of a Directed Graph

To create a directed graph (or digraph), use the DiGraph() method.

import networkx as nx
import matplotlib.pyplot as plt

G = nx.DiGraph()
G.add_edge('A', 'B')
G.add_edge('B', 'C')
G.add_edge('C', 'A')
G.add_edge('A', 'D')
G.add_edge('B', 'D')
G.add_edge('B', 'E')
G.add_edge('D', 'E')

nx.draw(G, with_labels=True, arrows=True)
plt.show()

To add edges, you use the same add_edge() method as with undirected graphs.

Alternatively, you can use this syntax to add multiple nodes and edges at once, using the add_nodes_from() and add_edges_from() methods respectively.

import networkx as nx
import matplotlib.pyplot as plt

G = nx.DiGraph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E'])
G.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'A'), ('A', 'D'), ('B', 'D'), ('B', 'E'), ('D', 'E')])

nx.draw(G, with_labels=True, arrows=True)
plt.show()

In both cases, the graph is processed with directed edges connecting the nodes.

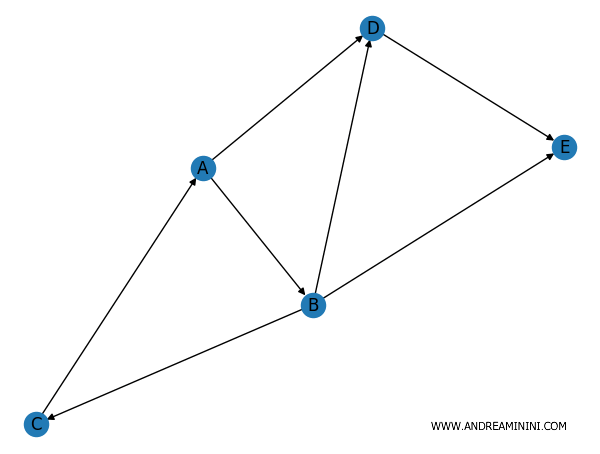
You can now calculate the in-degree, which is the number of edges entering a node.

in_degree = dict(G.in_degree())
print("In-degree:", in_degree)

In-degree: {'A': 1, 'B': 1, 'C': 1, 'D': 2, 'E': 2}

And also the out-degree of each node.

out_degree = dict(G.out_degree())
print("Out-degree:", out_degree)

Out-degree: {'A': 2, 'B': 3, 'C': 1, 'D': 1, 'E': 0}

You can easily identify the strongly connected components.

strong_components = list(nx.strongly_connected_components(G))
print(strong_components)

[{'E'}, {'D'}, {'A', 'C', 'B'}]

Multigraphs

It’s also possible to define a multigraph, which is a graph where nodes can have multiple edges connecting them.

To create a multigraph, use MultiGraph for undirected graphs and MultiDiGraph for directed graphs.

For example, define an undirected multigraph with three nodes and three edges.

import networkx as nx

MG = nx.MultiGraph()

# Add nodes
MG.add_nodes_from([1, 2, 3])

# Add multiple edges
MG.add_edge(1, 2, key='first')
MG.add_edge(1, 2, key='second')
MG.add_edge(2, 3, key='third')

In this graph, there are two edges between nodes 1 and 2, and one edge between nodes 2 and 3.

Here's the translated text:

List of Module Commands

Below is a comprehensive list of methods, functions, and instructions for the networkx module.

• AmbiguousSolution
• ArborescenceIterator
• DiGraph
• EdgePartition
• ExceededMaxIterations
• Graph
• GraphMLReader
• GraphMLWriter
• HasACycle
• LCF_graph
• LFR_benchmark_graph
• MultiDiGraph
• MultiGraph
• NetworkXAlgorithmError
• NetworkXError
• NetworkXException
• NetworkXNoCycle
• NetworkXNoPath
• NetworkXNotImplemented
• NetworkXPointlessConcept
• NetworkXTreewidthBoundExceeded
• NetworkXUnbounded
• NetworkXUnfeasible
• NodeNotFound
• NotATree
• PlanarEmbedding
• PowerIterationFailedConvergence
• SpanningTreeIterator
• __builtins__
• __cached__
• __doc__
• __file__
• __loader__
• __name__
• __package__
• __path__
• __spec__
• __version__
• _clear_cache
• _dispatchable
• _lazy_import
• adamic_adar_index
• add_cycle
• add_path
• add_star
• adjacency
• adjacency_data
• adjacency_graph
• adjacency_matrix
• adjacency_spectrum
• adjlist
• algebraic_connectivity
• algebraicconnectivity
• algorithms
• all
• all_neighbors
• all_node_cuts
• all_pairs_all_shortest_paths
• all_pairs_bellman_ford_path
• all_pairs_bellman_ford_path_length
• all_pairs_dijkstra
• all_pairs_dijkstra_path
• all_pairs_dijkstra_path_length
• all_pairs_lowest_common_ancestor
• all_pairs_node_connectivity
• all_pairs_shortest_path
• all_pairs_shortest_path_length
• all_shortest_paths
• all_simple_edge_paths
• all_simple_paths
• all_topological_sorts
• all_triads
• all_triplets
• ancestors
• antichains
• approximate_current_flow_betweenness_centrality
• approximation
• arf_layout
• articulation_points
• assortativity
• astar
• astar_path
• astar_path_length
• asteroidal
• atlas
• attr_matrix
• attr_sparse_matrix
• attracting
• attracting_components
• attribute_assortativity_coefficient
• attribute_mixing_dict
• attribute_mixing_matrix
• attrmatrix
• average_clustering
• average_degree_connectivity
• average_neighbor_degree
• average_node_connectivity
• average_shortest_path_length
• balanced_tree
• barabasi_albert_graph
• barbell_graph
• barycenter
• beamsearch
• bellman_ford_path
• bellman_ford_path_length
• bellman_ford_predecessor_and_distance
• bethe_hessian_matrix
• bethe_hessian_spectrum
• bethehessianmatrix
• betweenness
• betweenness_centrality
• betweenness_centrality_subset
• betweenness_subset
• bfs_beam_edges
• bfs_edges
• bfs_labeled_edges
• bfs_layers
• bfs_layout
• bfs_predecessors
• bfs_successors
• bfs_tree
• biconnected
• biconnected_component_edges
• biconnected_components
• bidirectional_dijkstra
• bidirectional_shortest_path
• binary
• binomial_graph
• binomial_tree
• bipartite
• bipartite_layout
• boundary
• boundary_expansion
• breadth_first_search
• bridges
• broadcasting
• bull_graph
• capacity_scaling
• cartesian_product
• caveman_graph
• cd_index
• center
• centrality
• chain_decomposition
• chains
• check_planarity
• chordal
• chordal_cycle_graph
• chordal_graph_cliques
• chordal_graph_treewidth
• chordless_cycles
• chromatic_polynomial
• chvatal_graph
• circulant_graph
• circular_ladder_graph
• circular_layout
• classes
• classic
• clique
• closeness
• closeness_centrality
• closeness_vitality
• cluster
• clustering
• cn_soundarajan_hopcroft
• cographs
• coloring
• combinatorial_embedding_to_pos
• common_neighbor_centrality
• common_neighbors
• communicability
• communicability_alg
• communicability_betweenness_centrality
• communicability_exp
• community
• complement
• complete_bipartite_graph
• complete_graph
• complete_multipartite_graph
• complete_to_chordal_graph
• components
• compose
• compose_all
• compute_v_structures
• condensation
• conductance
• config
• configuration_model
• connected
• connected_caveman_graph
• connected_components
• connected_double_edge_swap
• connected_watts_strogatz_graph
• connectivity
• constraint
• contracted_edge
• contracted_nodes
• convert
• convert_matrix
• convert_node_labels_to_integers
• core
• core_number
• coreviews
• corona_product
• correlation
• cost_of_flow
• could_be_isomorphic
• covering
• create_empty_copy
• cubical_graph
• current_flow_betweenness
• current_flow_betweenness_centrality
• current_flow_betweenness_centrality_subset
• current_flow_betweenness_subset
• current_flow_closeness
• current_flow_closeness_centrality
• cut_size
• cuts
• cycle_basis
• cycle_graph
• cycles
• cytoscape
• cytoscape_data
• cytoscape_graph
• d_separated
• d_separation
• dag
• dag_longest_path
• dag_longest_path_length
• dag_to_branching
• davis_southern_women_graph
• dedensify
• degree
• degree_alg
• degree_assortativity_coefficient
• degree_centrality
• degree_histogram
• degree_mixing_dict
• degree_mixing_matrix
• degree_pearson_correlation_coefficient
• degree_seq
• degree_sequence_tree
• dense
• dense_gnm_random_graph
• density
• depth_first_search
• desargues_graph
• descendants
• descendants_at_distance
• dfs_edges
• dfs_labeled_edges
• dfs_postorder_nodes
• dfs_predecessors
• dfs_preorder_nodes
• dfs_successors
• dfs_tree
• diameter
• diamond_graph
• difference
• digraph
• dijkstra_path
• dijkstra_path_length
• dijkstra_predecessor_and_distance
• directed
• directed_combinatorial_laplacian_matrix
• directed_configuration_model
• directed_edge_swap
• directed_havel_hakimi_graph
• directed_joint_degree_graph
• directed_laplacian_matrix
• directed_modularity_matrix
• disjoint_union
• disjoint_union_all
• dispersion
• distance_measures
• distance_regular
• dodecahedral_graph
• dominance
• dominance_frontiers
• dominating
• dominating_set
• dorogovtsev_goltsev_mendes_graph
• double_edge_swap
• draw
• draw_circular
• draw_kamada_kawai
• draw_networkx
• draw_networkx_edge_labels
• draw_networkx_edges
• draw_networkx_labels
• draw_networkx_nodes
• draw_planar
• draw_random
• draw_shell
• draw_spectral
• draw_spring
• drawing
• dual_barabasi_albert_graph
• duplication
• duplication_divergence_graph
• eccentricity
• edge_betweenness_centrality
• edge_betweenness_centrality_subset
• edge_bfs
• edge_boundary
• edge_connectivity
• edge_current_flow_betweenness_centrality
• edge_current_flow_betweenness_centrality_subset
• edge_dfs
• edge_disjoint_paths
• edge_expansion
• edge_load_centrality
• edge_subgraph
• edgebfs
• edgedfs
• edgelist
• edges
• effective_graph_resistance
• effective_size
• efficiency
• efficiency_measures
• ego
• ego_graph
• eigenvector
• eigenvector_centrality
• eigenvector_centrality_numpy
• empty_graph
• enumerate_all_cliques
• equitable_color
• equivalence_classes
• erdos_renyi_graph
• estrada_index
• euler
• eulerian_circuit
• eulerian_path
• eulerize
• exception
• expanders
• expected_degree_graph
• extended_barabasi_albert_graph
• fast_could_be_isomorphic
• fast_gnp_random_graph
• faster_could_be_isomorphic
• fiedler_vector
• filters
• find_asteroidal_triple
• find_cliques
• find_cliques_recursive
• find_cycle
• find_induced_nodes
• find_minimal_d_separator
• find_negative_cycle
• florentine_families_graph
• flow
• flow_hierarchy
• flow_matrix
• floyd_warshall
• floyd_warshall_numpy
• floyd_warshall_predecessor_and_distance
• forest_str
• freeze
• from_dict_of_dicts
• from_dict_of_lists
• from_edgelist
• from_graph6_bytes
• from_nested_tuple
• from_numpy_array
• from_pandas_adjacency
• from_pandas_edgelist
• from_prufer_sequence
• from_scipy_sparse_array
• from_sparse6_bytes
• frucht_graph
• fruchterman_reingold_layout
• full_join
• full_rary_tree
• function
• gaussian_random_partition_graph
• general_random_intersection_graph
• generalized_degree
• generate_adjlist
• generate_edgelist
• generate_gexf
• generate_gml
• generate_graphml
• generate_multiline_adjlist
• generate_network_text
• generate_pajek
• generate_random_paths
• generators
• generic
• generic_bfs_edges
• geographical_threshold_graph
• geometric
• geometric_edges
• geometric_soft_configuration_graph
• get_edge_attributes
• get_node_attributes
• gexf
• girth
• global_efficiency
• global_parameters
• global_reaching_centrality
• gml
• gn_graph
• gnc_graph
• gnm_random_graph
• gnp_random_graph
• gnr_graph
• goldberg_radzik
• gomory_hu_tree
• google_matrix
• graph
• graph6
• graph_atlas
• graph_atlas_g
• graph_edit_distance
• graph_hashing
• graphical
• graphmatrix
• graphml
• graphviews
• greedy_color
• grid_2d_graph
• grid_graph
• group
• group_betweenness_centrality
• group_closeness_centrality
• group_degree_centrality
• group_in_degree_centrality
• group_out_degree_centrality
• gutman_index
• harary_graph
• harmonic
• harmonic_centrality
• has_bridges
• has_eulerian_path
• has_path
• havel_hakimi_graph
• heawood_graph
• hexagonal_lattice_graph
• hierarchy
• hits
• hits_alg
• hkn_harary_graph
• hnm_harary_graph
• hoffman_singleton_graph
• house_graph
• house_x_graph
• hybrid
• hypercube_graph
• icosahedral_graph
• identified_nodes
• immediate_dominators
• in_degree_centrality
• incidence_matrix
• incremental_closeness_centrality
• induced_subgraph
• information_centrality
• internet_as_graphs
• intersection
• intersection_all
• intersection_array
• interval_graph
• inverse_line_graph
• is_aperiodic
• is_arborescence
• is_at_free
• is_attracting_component
• is_biconnected
• is_bipartite
• is_branching
• is_chordal
• is_connected
• is_d_separator
• is_digraphical
• is_directed
• is_directed_acyclic_graph
• is_distance_regular
• is_dominating_set
• is_edge_cover
• is_empty
• is_eulerian
• is_forest
• is_frozen
• is_graphical
• is_isolate
• is_isomorphic
• is_k_edge_connected
• is_k_regular
• is_kl_connected
• is_matching
• is_maximal_matching
• is_minimal_d_separator
• is_multigraphical
• is_negatively_weighted
• is_path
• is_perfect_matching
• is_planar
• is_pseudographical
• is_regular
• is_regular_expander
• is_semiconnected
• is_semieulerian
• is_simple_path
• is_strongly_connected
• is_strongly_regular
• is_tournament
• is_tree
• is_triad
• is_valid_degree_sequence_erdos_gallai
• is_valid_degree_sequence_havel_hakimi
• is_valid_directed_joint_degree
• is_valid_joint_degree
• is_weakly_connected
• is_weighted
• isolate
• isolates
• isomorphism
• jaccard_coefficient
• johnson
• join
• join_trees
• joint_degree_graph
• joint_degree_seq
• json_graph
• junction_tree
• k_components
• k_core
• k_corona
• k_crust
• k_edge_augmentation
• k_edge_components
• k_edge_subgraphs
• k_factor
• k_random_intersection_graph
• k_shell
• k_truss
• kamada_kawai_layout
• karate_club_graph
• katz
• katz_centrality
• katz_centrality_numpy
• kemeny_constant
• kl_connected_subgraph
• kneser_graph
• kosaraju_strongly_connected_components
• krackhardt_kite_graph
• ladder_graph
• laplacian
• laplacian_centrality
• laplacian_matrix
• laplacian_spectrum
• laplacianmatrix
• lattice
• lattice_reference
• layout
• lazy_imports
• leda
• les_miserables_graph
• lexicographic_product
• lexicographical_topological_sort
• linalg
• line
• line_graph
• link_analysis
• link_prediction
• load
• load_centrality
• local_bridges
• local_constraint
• local_efficiency
• local_reaching_centrality
• lollipop_graph
• lowest_common_ancestor
• lowest_common_ancestors
• make_clique_bipartite
• make_max_clique_graph
• margulis_gabber_galil_graph
• matching
• max_flow_min_cost
• max_weight_clique
• max_weight_matching
• maximal_independent_set
• maximal_matching
• maximum_branching
• maximum_flow
• maximum_flow_value
• maximum_spanning_arborescence
• maximum_spanning_edges
• maximum_spanning_tree
• maybe_regular_expander
• min_cost_flow
• min_cost_flow_cost
• min_edge_cover
• min_weight_matching
• minimal_d_separator
• minimum_branching
• minimum_cut
• minimum_cut_value
• minimum_cycle_basis
• minimum_edge_cut
• minimum_node_cut
• minimum_spanning_arborescence
• minimum_spanning_edges
• minimum_spanning_tree
• minors
• mis
• mixing
• mixing_dict
• mixing_expansion
• modular_product
• modularity_matrix
• modularity_spectrum
• modularitymatrix
• moebius_kantor_graph
• moral
• moral_graph
• multi_source_dijkstra
• multi_source_dijkstra_path
• multi_source_dijkstra_path_length
• multidigraph
• multigraph
• multiline_adjlist
• multipartite_layout
• mycielski
• mycielski_graph
• mycielskian
• navigable_small_world_graph
• negative_edge_cycle
• neighbor_degree
• neighbors
• network_simplex
• newman_watts_strogatz_graph
• node_attribute_xy
• node_boundary
• node_classification
• node_clique_number
• node_connected_component
• node_connectivity
• node_degree_xy
• node_disjoint_paths
• node_expansion
• node_link
• node_link_data
• node_link_graph
• nodes
• nodes_with_selfloops
• non_edges
• non_neighbors
• non_randomness
• nonisomorphic_trees
• normalized_cut_size
• normalized_laplacian_matrix
• normalized_laplacian_spectrum
• null_graph
• number_attracting_components
• number_connected_components
• number_of_cliques
• number_of_edges
• number_of_isolates
• number_of_nodes
• number_of_nonisomorphic_trees
• number_of_selfloops
• number_of_spanning_trees
• number_of_walks
• number_strongly_connected_components
• number_weakly_connected_components
• numeric_assortativity_coefficient
• nx_agraph
• nx_latex
• nx_pydot
• nx_pylab
• octahedral_graph
• omega
• onion_layers
• operators
• optimal_edit_paths
• optimize_edit_paths
• optimize_graph_edit_distance
• out_degree_centrality
• overall_reciprocity
• pagerank
• pagerank_alg
• pairs
• pajek
• paley_graph
• panther_similarity
• pappus_graph
• parse_adjlist
• parse_edgelist
• parse_gml
• parse_graphml
• parse_leda
• parse_multiline_adjlist
• parse_pajek
• partial_duplication_graph
• partition_spanning_tree
• path_graph
• path_weight
• percolation
• percolation_centrality
• periphery
• petersen_graph
• planar_drawing
• planar_layout
• planarity
• planted_partition_graph
• polynomials
• power
• powerlaw_cluster_graph
• predecessor
• preferential_attachment
• prefix_tree
• prefix_tree_recursive
• product
• projected_graph
• prominent_group
• quotient_graph
• ra_index_soundarajan_hopcroft
• radius
• random_clustered
• random_clustered_graph
• random_cograph
• random_degree_sequence_graph
• random_geometric_graph
• random_graphs
• random_internet_as_graph
• random_k_out_graph
• random_kernel_graph
• random_labeled_rooted_forest
• random_labeled_rooted_tree
• random_labeled_tree
• random_layout
• random_lobster
• random_partition_graph
• random_powerlaw_tree
• random_powerlaw_tree_sequence
• random_reference
• random_regular_expander_graph
• random_regular_graph
• random_shell_graph
• random_spanning_tree
• random_tree
• random_triad
• random_unlabeled_rooted_forest
• random_unlabeled_rooted_tree
• random_unlabeled_tree
• reaching
• read_adjlist
• read_edgelist
• read_gexf
• read_gml
• read_graph6
• read_graphml
• read_leda
• read_multiline_adjlist
• read_pajek
• read_sparse6
• read_weighted_edgelist
• readwrite
• reciprocity
• reconstruct_path
• recursive_simple_cycles
• regular
• relabel
• relabel_gexf_graph
• relabel_nodes
• relaxed_caveman_graph
• reportviews
• rescale_layout
• rescale_layout_dict
• resistance_distance
• resource_allocation_index
• restricted_view
• reverse
• reverse_view
• rich_club_coefficient
• richclub
• ring_of_cliques
• rooted_product
• s_metric
• scale_free_graph
• schultz_index
• second_order
• second_order_centrality
• sedgewick_maze_graph
• selfloop_edges
• semiconnected
• set_edge_attributes
• set_node_attributes
• shell_layout
• shortest_path
• shortest_path_length
• shortest_paths
• shortest_simple_paths
• sigma
• similarity
• simple_cycles
• simple_paths
• simrank_similarity
• single_source_all_shortest_paths
• single_source_bellman_ford
• single_source_bellman_ford_path
• single_source_bellman_ford_path_length
• single_source_dijkstra
• single_source_dijkstra_path
• single_source_dijkstra_path_length
• single_source_shortest_path
• single_source_shortest_path_length
• single_target_shortest_path
• single_target_shortest_path_length
• small
• smallworld
• smetric
• snap_aggregation
• social
• soft_random_geometric_graph
• spanner
• sparse6
• sparsifiers
• spectral_bisection
• spectral_graph_forge
• spectral_layout
• spectral_ordering
• spectrum
• spiral_layout
• spring_layout
• square_clustering
• star_graph
• stochastic
• stochastic_block_model
• stochastic_graph
• stoer_wagner
• strong_product
• strongly_connected
• strongly_connected_components
• strongly_connected_components_recursive
• structuralholes
• subgraph
• subgraph_alg
• subgraph_centrality
• subgraph_centrality_exp
• subgraph_view
• sudoku
• sudoku_graph
• summarization
• swap
• symmetric_difference
• tadpole_graph
• tensor_product
• tetrahedral_graph
• text
• thresholded_random_geometric_graph
• time_dependent
• time_series
• to_dict_of_dicts
• to_dict_of_lists
• to_directed
• to_edgelist
• to_graph6_bytes
• to_latex
• to_latex_raw
• to_nested_tuple
• to_networkx_graph
• to_numpy_array
• to_pandas_adjacency
• to_pandas_edgelist
• to_prufer_sequence
• to_scipy_sparse_array
• to_sparse6_bytes
• to_undirected
• topological_generations
• topological_sort
• total_spanning_tree_weight
• tournament
• transitive_closure
• transitive_closure_dag
• transitive_reduction
• transitivity
• traversal
• tree
• tree_all_pairs_lowest_common_ancestor
• tree_broadcast_center
• tree_broadcast_time
• tree_data
• tree_graph
• trees
• triad_graph
• triad_type
• triadic_census
• triads
• triads_by_type
• triangles
• triangular_lattice_graph
• trivial_graph
• trophic
• trophic_differences
• trophic_incoherence_parameter
• trophic_levels
• truncated_cube_graph
• truncated_tetrahedron_graph
• turan_graph
• tutte_graph
• tutte_polynomial
• unary
• uniform_random_intersection_graph
• union
• union_all
• unweighted
• utils
• vf2pp_all_isomorphisms
• vf2pp_is_isomorphic
• vf2pp_isomorphism
• visibility_graph
• vitality
• volume
• voronoi
• voronoi_cells
• voterank
• voterank_alg
• walks
• watts_strogatz_graph
• waxman_graph
• weakly_connected
• weakly_connected_components
• weighted
• weisfeiler_lehman_graph_hash
• weisfeiler_lehman_subgraph_hashes
• wheel_graph
• wiener
• wiener_index
• windmill_graph
• within_inter_cluster
• write_adjlist
• write_edgelist
• write_gexf
• write_gml
• write_graph6
• write_graphml
• write_graphml_lxml
• write_graphml_xml
• write_latex
• write_multiline_adjlist
• write_network_text
• write_pajek
• write_sparse6
• write_weighted_edgelist

And so on.