Calculating Maximum Flow in a Graph with Python
In this tutorial, I will demonstrate how to calculate the maximum flow in a graph using Python's networkx module.
Maximum flow is the highest amount of flow that can be transported from a source node to a destination node in a directed graph.
First, let's import the networkx module.
import networkx as nx
Next, we define a directed graph.
G = nx.DiGraph()
We then add the edges to the graph, specifying the capacity for each one.
G.add_edge('A', 'B', capacity=4)
G.add_edge('B', 'C', capacity=3)
G.add_edge('C', 'A', capacity=2)
G.add_edge('A', 'D', capacity=2)
G.add_edge('B', 'D', capacity=3)
G.add_edge('B', 'E', capacity=4)
G.add_edge('D', 'E', capacity=3)
We can visualize the graph along with its capacities.
import matplotlib.pyplot as plt
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='lightblue')
labels = nx.get_edge_attributes(G, 'capacity')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.show()
Below is the directed graph with capacities labeled on each edge.
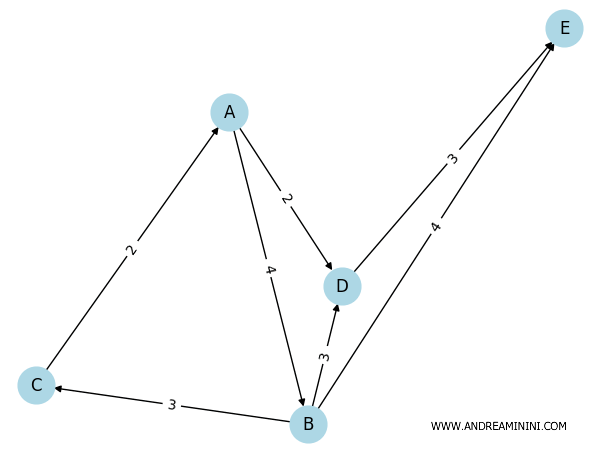
To calculate the maximum flow between two nodes, we use the maximum_flow() function from networkx.
We specify node A as the source and node E as the sink.
Now, let's compute the maximum flow from A to E.
flow_value, flow_dict = nx.maximum_flow(G, 'A', 'E')
print(f"Maximum flow from A to E: {flow_value}")
print("Flow details for each edge:")
for u, v in flow_dict.items():
print(f"{u} -> {v}")
The result shows the maximum flow value and the flow through each edge. Here is an example of the expected output:
Maximum flow from A to E: 6
Flow details for each edge:
A -> {'B': 4, 'D': 2}
B -> {'C': 0, 'D': 0, 'E': 4}
C -> {'A': 0}
D -> {'E': 2}
E -> {}
The maximum flow is 6 because from node A, 4 units of flow can go to node B, and 2 units can go to node D.
- A->B: 4
- A->D: 2
From node B, all 4 units can be sent to node E since the capacity of the edge (B, E) is 4.
- B->E: 4
From node D, all 2 units can be sent to node E because the capacity of the edge (D, E) is 3, which is sufficient.
- D->E: 2
In total, 4 + 2 = 6 units of flow reach the destination node E.
When calculating the maximum flow in a graph using networkx, it's crucial to have well-defined capacities on the edges; otherwise, the calculation won't be accurate.
And that's it!
