Exponential inequalities

An inequality is called an exponential inequality when the unknown variable appears in the exponent of one or more exponential expressions.

These inequalities can be solved directly whenever the exponential terms on both sides have the same base.

$$ b^x > b^y $$

In this setting, the inequality can be reduced to a direct comparison of the exponents.

• If the base is greater than 1, the inequality between the exponents preserves its direction $$ x > y $$
• If the base lies between 0 and 1, that is 0<a<1, the inequality between the exponents is reversed $$ x < y $$

A practical example

Example 1

In this inequality, the unknown x appears as the exponent of an exponential expression.

$$ 5^x > 125 $$

Both sides can be rewritten as powers of 5.

I can therefore express the inequality as

$$ 5^x > 5^3 $$

Since the bases are identical, the comparison can be carried out directly between the exponents.

$$ x > 3 $$

The base is greater than 1, so the direction of the inequality remains unchanged.

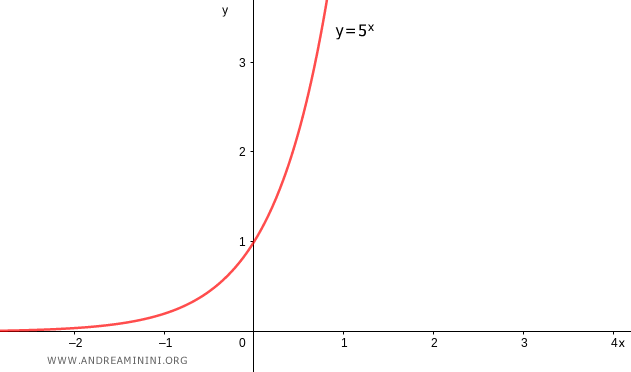
In this case, the graph of the exponential function is increasing, indicating a direct relationship between the exponent and the function value.

Example 2

Here again, the unknown x appears in the exponent.

$$ (\frac{1}{5})^x > (\frac{1}{125}) $$

I rewrite the inequality using a common base

$$ (\frac{1}{5})^x > (\frac{1}{5})^3 $$

In this case, the base is positive but strictly less than 1.

The graph of the exponential function is decreasing.

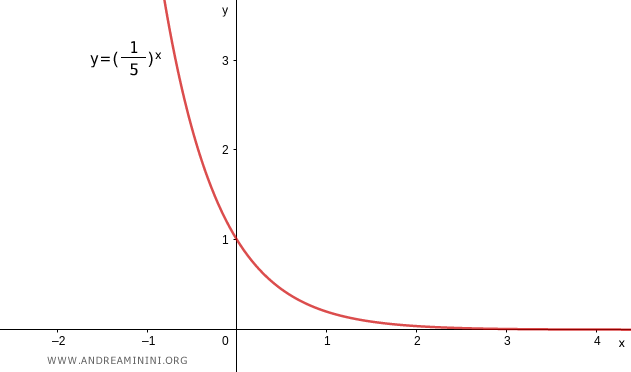
As a consequence, the inequality between the exponents is reversed

$$ x < 3 $$

Solving exponential inequalities using logarithms

In some situations, exponential inequalities can be solved by means of logarithms.

This method applies only when both sides of the inequality are positive, since the logarithm of a nonpositive number is not defined.

Example

Let us return to the example considered above

$$ 5^{x} > 125 $$

Both sides of the inequality are positive, so the logarithmic approach is applicable.

I take the logarithm base 5 of both sides

$$ \log_5 5^{x} > \log_5 125 $$

Note. Any logarithmic base could be used. Base 5 is chosen here because it simplifies the final expression.

By the properties of logarithms, the exponent x can be factored out of the logarithm

$$ x \cdot \log_5 5 > \log_5 125 $$

I now divide both sides by log₅ 5.

Since the divisor is positive, the direction of the inequality is preserved.

$$ \frac{ x \cdot \log_5 5 }{\log_5 5} > \frac{ \log_5 125 }{ \log_5 5 } $$

Note. If the divisor were negative, the direction of the inequality would need to be reversed.

In this way, x is isolated

$$ x > \frac{ \log_5 125 }{ \log_5 5 } $$

Knowing that log₅ 125 = 3 and log₅ 5 = 1

$$ x > \frac{ 3 }{ 1 } $$

$$ x > 3 $$

The final result coincides with the one obtained earlier.

And so on.