Integer Operations

Within the set of integers ℤ, the following fundamental operations are defined.

Addition

Given two integers a and b, their sum is an integer c defined by c = a + b. $$ c=a+b $$

To compute the sum of two integers, one must determine whether the numbers have the same sign or opposite signs.

• Sum of integers with the same sign
  The sum of two integers with the same sign is equal to the sum of the absolute values of the addends and has the common sign of the addends.

  Example. $$ 2+3 = + (|2|+|3|) = + (2+3) = +5 $$

• Sum of integers with different signs
  The sum of two integers with different signs is equal to the difference between the larger and the smaller absolute values, and it takes the sign of the addend with the greater absolute value.

  Example. $$ -3+5 = + (|5|-|-3|) = + (5-3) = +2 $$

Addition is a closed operation in the set of integers, since the sum of any two integers is always an integer.

Addition of integers satisfies both the commutative and associative properties.

$$ a+b=b+a $$

$$ a+(b+c)=(a+b)+c $$

The number zero is the identity element for addition, because adding zero to any integer leaves the integer unchanged.

$$ a+0=0+a=a $$

Subtraction

The difference between two integers a and b is defined as the algebraic sum of the minuend (a) and the additive inverse of the subtrahend (-b). $$ a-b = a+(-b) $$ The result of a subtraction is called the difference.

Subtraction is the inverse operation of addition.

Example. The subtraction of the integers 23 and 14 $$ 23 - 14 $$ can be rewritten as the algebraic sum of the minuend (23) and the additive inverse of the subtrahend (-14). $$ 23 + (-14) $$ Applying the rules of addition yields $$ 23 + (-14) = +9 $$ The difference is +9.

Subtraction is a closed operation in the set of integers, because the difference of any two integers is always an integer.

$$ \forall \ a,b \in \mathbb{Z} \Rightarrow a-b \in \mathbb{Z} $$

Note. Subtraction is not a closed operation in the set of natural numbers (N), since the difference of two natural numbers may be negative, and negative integers do not belong to N. $$ 14 - 23 = 14 + (-23) = -9 \notin N $$ Consequently, when working within the natural numbers, the minuend must be greater than or equal to the subtrahend. This restriction does not apply in the set of integers ℤ.

The difference between two integers satisfies the invariance property.

Adding or subtracting the same integer c to both the minuend (a) and the subtrahend (b) leaves the difference unchanged.

$$ a-b = (a+c) - (b+c) $$

$$ a-b = (a-c) - (b-c) $$

Multiplication

The product of two integers a ⋅ b is an integer equal to the product of the absolute values of the factors. The result is positive if the factors have the same sign, and negative if they have different signs.

The sign rule for multiplication is straightforward.

It is commonly summarized in the following table.

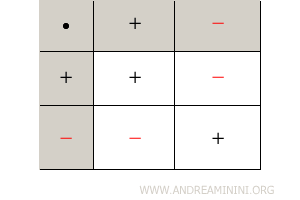
Example. In the product of 3 and -4 $$ 3 \cdot (-4) $$ the factors have opposite signs, so the product is negative. $$ - (|3| \cdot |-4|) = - (3 \cdot 4) = -12 $$

The sign rule extends naturally to products involving more than two factors.

In particular, the product is positive if the number of negative factors is even.

If the number of negative factors is odd, the product is negative.

Example. In the product of 3, -4, and -2, the number of negative factors is even, so the product is positive. $$ + (|3| \cdot |-4| \cdot |-2|) = + (3 \cdot 4 \cdot 2) = +24 $$

Multiplication is a closed operation in the set of integers ℤ, because the product of any two integers is itself an integer.

$$ \forall \ a,b \in \mathbb{Z} \Rightarrow a \cdot b \in \mathbb{Z} $$

Multiplication of integers satisfies the commutative property.

$$ a \cdot b = b \cdot a $$

Example. $$ 2 \cdot (-4) = (-4) \cdot 2 = -8 $$

Multiplication of integers also satisfies the associative property.

$$ a \cdot (b \cdot c) = (a \cdot b) \cdot c $$

Example. $$ -2 \cdot (4 \cdot 3) = (-2 \cdot 4) \cdot 3 = -24 $$

Multiplication of integers satisfies the distributive property with respect to addition.

$$ a \cdot (b + c) = a \cdot b + a \cdot c $$

Example. $$ -2 \cdot (4 + 3) = -2 \cdot 4 + (-2) \cdot 3 = -14 $$

The identity element for multiplication is the integer +1.

Multiplying any integer by +1 leaves the integer unchanged.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a \cdot 1 = a $$

Example. $$ 4 \cdot 1 = + ( |4| \cdot |1| ) = + (4 \cdot 1) = 4 $$

Multiplying any integer by -1 yields its additive inverse.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a \cdot (-1) = -a $$

Example. $$ 4 \cdot (-1) = - ( |4| \cdot |-1| ) = - (4 \cdot 1) = -4 $$

The absorbing element for multiplication is 0, because the product of any integer and zero is zero.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a \cdot 0 = 0 \cdot a = 0 $$

As a consequence, multiplication of integers satisfies the zero-product property.

Example. $$ 4 \cdot 0 = 0 \cdot 4 = 0 $$

Division

The division of two integers a and b, with b ≠ 0, produces a rational number called the quotient. $$ a:b = q \in \mathbb{Q} $$ Here, a is the dividend and b is the divisor.

Division is the inverse operation of multiplication.

If the dividend a can be written as a = k ⋅ b, meaning that a is a multiple of the divisor, then the quotient is an integer.

$$ \forall \ a,b,k \in \mathbb{Z} \ , \ a = k \cdot b \ \Rightarrow a:b = (k \cdot b):b = k \in \mathbb{Z} $$

In the general case, dividing two integers a:b with b ≠ 0 yields the quotient of their absolute values |a|:|b|, with the sign determined by the sign rules for multiplication.

For this reason, the computational procedure for division closely mirrors that of multiplication.

Example. Dividing 8 by -2 gives the integer -4. $$ \frac{8}{-2} = - \left( \frac{|8|}{|2|} \right) = - \left( \frac{8}{2} \right) = -4 $$ The dividend is positive and the divisor is negative. Since the signs differ, the quotient is negative.

Division satisfies the invariance property.

Multiplying or dividing both the dividend and the divisor by the same nonzero integer k ≠ 0 leaves the value of the quotient unchanged.

$$ a:b = (a \cdot k):(b \cdot k) $$

This property is often clearer when expressed in fractional form.

$$ \frac{a}{b} = \frac{a}{b} \cdot 1 = \frac{a}{b} \cdot \frac{k}{k} = \frac{a \cdot k}{b \cdot k} $$

Example. The quotient of the division 8:2 is 4. $$ \frac{8}{2} = 4 $$ If both the dividend and the divisor are multiplied by k = 3, the quotient remains the same. $$ \frac{8 \cdot 3}{2 \cdot 3} = \frac{24}{6} = 4 $$

Division satisfies the right distributive property with respect to addition.

$$ (a+b):c = a:c + b:c $$

Example. The division of (6 + 2) by 2 $$ (6+2):2 = 8:2 = 4 $$ can be evaluated using right distributivity. $$ (6+2):2 = 6:2 + 2:2 = 3 + 1 = 4 $$

However, division does not satisfy the left distributive property with respect to addition.

$$ c:(a+b) \ne c:a + c:b $$

Example. Dividing 12 by (4 + 2) gives 2. $$ 12:(4+2) = 12:6 = 2 $$ This result cannot be obtained by applying left distributivity. $$ 12:(4+2) = 2 \ne 12:4 + 12:2 = 3 + 6 = 9 $$

Division is not a closed operation in the set of integers, because the quotient may be a rational number.

$$ \forall \ a,b \in \mathbb{Z} \ , \ b \ne 0 \Rightarrow a:b \in \mathbb{Q} $$

Moreover, division by zero is not defined. Expressions such as 0:0 are indeterminate, while expressions such as 5:0 are meaningless.

Example. Dividing 5 by 2 yields 2.5. $$ 5:2 = 2.5 $$ The quotient is not an integer. $$ 2.5 \notin \mathbb{Z} $$ It is a rational number. $$ 2.5 \in \mathbb{Q} $$

The identity element for division is 1, because dividing any integer by 1 leaves it unchanged.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a:1 = a $$

Example. $$ 4:1 = 4 \qquad -4:1 = -4 $$

Consequently, any nonzero integer divided by itself equals 1.

$$ \forall \ a \in \mathbb{Z} \ , \ a \ne 0 \Rightarrow a:a = 1 $$

Example. $$ 4:4 = 1 \qquad (-4):(-4) = 1 $$

Dividing any integer by -1 produces its additive inverse.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a:(-1) = -a $$

Example. $$ 4:(-1) = -4 \qquad (-4):(-1) = 4 $$

Powers

The power of a nonzero integer a ≠ 0 raised to a natural exponent n has an absolute value equal to |a| raised to the same exponent, and its sign is determined as follows:


• negative (-) if the base is negative and the exponent is odd
• positive (+) in all other cases

The sign of an integer power follows the sign rules for multiplication.

Example. Consider the power $$ (-3)^5 $$ The base is negative and the exponent is odd, so the result is negative. $$ (-3)^5 = - (|-3|)^5 = - (3^5) = -243 $$ The same result follows from repeated multiplication. $$ (-3)^5 = (-3)\cdot(-3)\cdot(-3)\cdot(-3)\cdot(-3) = -243 $$ Since the negative sign appears an odd number of times, the power is negative.

If the base is zero, any power with a positive integer exponent is equal to zero.

$$ 0^n = 0 \quad \text{with } n \in \mathbb{Z}, \ n > 0 $$

If the exponent is equal to 1, the power of an integer coincides with the integer itself.

$$ \forall \ a \in \mathbb{Z} \Rightarrow a^1 = a $$

Example. $$ 4^1 = 4 $$

If the exponent is -1, the power of a nonzero integer is equal to its reciprocal.

$$ \forall \ a \in \mathbb{Z} \ , \ a \ne 0 \Rightarrow a^{-1} = \frac{1}{a} $$

Example. $$ 4^{-1} = \frac{1}{4} $$

If the exponent is 0 and the base is nonzero, the power is equal to 1.

$$ \forall \ a \in \mathbb{Z} \ , \ a \ne 0 \Rightarrow a^0 = 1 $$

For further discussion, see the proof.

Example. $$ 4^0 = 1 $$

If both the base and the exponent are zero, the expression is undefined.

$$ 0^0 = \text{undefined} $$

For further discussion, see the proof.

If the base is zero and the exponent is a negative integer, the operation is impossible, as it corresponds to division by zero.

$$ \forall \ n \in \mathbb{Z} \ , \ n < 0 \Rightarrow 0^n = \text{impossible} $$

Example. $$ 0^{-1} = \frac{1}{0^1} = \text{impossible} $$

A subtle but important point concerns the precedence of exponentiation.

Exponentiation always takes precedence over the sign when parentheses are not used.

Example. $$ (-4)^2 = (-4)\cdot(-4) = 16 $$ whereas $$ -4^2 = - (4 \cdot 4) = -16 $$ Therefore, $$ (-4)^2 \ne -4^2 $$

And so on.