Integers
The integers form the set that includes the natural numbers (0, 1, 2, 3, ...) together with their negative counterparts (-1, -2, -3, ...). This set is denoted by the symbol Z and is commonly referred to as the set of signed integers.
From a conceptual point of view, integers can be understood as all possible differences between natural numbers.
$$ p - q \in Z $$
where p and q are any natural numbers.
The set of integers
The introduction of negative numbers extends the set of natural numbers, making it possible to represent quantities such as debts, losses, or movements in opposite directions.
For every nonzero natural number, there are exactly two corresponding integers: one positive and one negative.
Example. The natural number 2 corresponds to the two integers +2 and -2.
Integers are commonly represented on an oriented number line, where values increase from left to right.
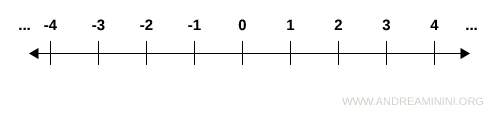
Unlike natural numbers, every integer z ∈ Z has both a predecessor, z - 1, and a successor, z + 1.
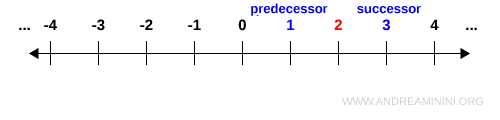
The distance between any integer and its predecessor or successor is always equal to 1.
Moreover, between an integer and its immediate successor (or predecessor), no other integers exist.
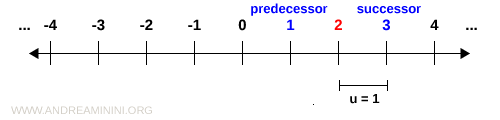
The set of all integers is denoted by the capital letter Z.
$$ Z = \{ \ldots, -3, -2, -1, 0, 1, 2, 3, \ldots \} $$
The nonzero integers can be divided into two distinct subsets.
- Positive integers
Integers with a positive sign are called positive integers. The set of positive integers is denoted by Z⁺. $$ Z^+ = \{1, 2, 3, \ldots \} $$ These are all the integers greater than zero.
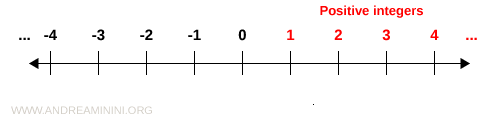
- Negative integers
Integers with a negative sign are called negative integers. The set of negative integers is denoted by Z⁻. $$ Z^- = \{ \ldots, -3, -2, -1 \} $$ These are all the integers less than zero.
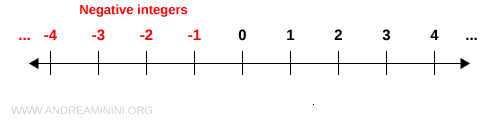
Integers with the same sign are called like-signed.
Integers with different signs are called unlike-signed.
Example. The integers +2 and +4 are like-signed. The integers +2 and -1, by contrast, are unlike-signed.
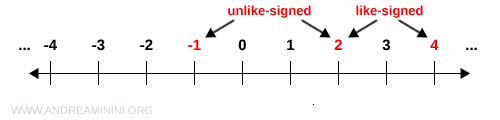
Two integers are called opposites, or additive inverses, if they have the same absolute value and opposite signs.
The absolute value (or modulus) of a number represents its magnitude, independent of its sign.
Example. The integers +2 and -2 are opposites because they share the same absolute value, |+2| = 2 and |-2| = 2. Therefore, +2 and -2 are additive inverses.
What is the opposite of zero? To clarify this idea, recall the defining property of opposite numbers: the sum of two opposite integers is always zero. For instance, -2 + 2 = 0, -3 + 3 = 0, -4 + 4 = 0. From this, it follows that the opposite of zero is zero itself, since 0 + 0 = 0.
In summary, the set of integers has the following fundamental properties:
- Ordered set
The set of integers is ordered because, given any two integers, one can always determine whether one is greater than, less than, or equal to the other.Note. Among two positive integers, the one with the greater absolute value is larger. Among two negative integers, the one with the smaller absolute value is larger. Every positive integer is greater than any negative integer. Zero is greater than any negative integer and smaller than any positive integer.
- Infinite set
The set of integers Z is infinite because it contains infinitely many elements. - Discrete set
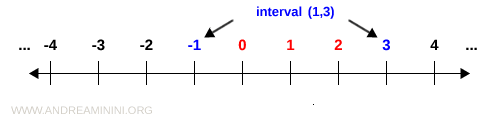
The set of integers is discrete because between any integer and its successor (or predecessor) there are no other integers. Consequently, between any two integers (a, b), there is always a finite number of integers.
Example. In the interval between the integers (-1, 3), there are exactly three integers: 0, 1, and 2.
Operations on integers
The following operations can be performed within the set of integers:
- Addition
$$ a + b = c \quad a, b, c \in Z $$ - Subtraction
$$ a - b = c \quad a, b, c \in Z $$ - Multiplication
$$ a \cdot b = c \quad a, b, c \in Z $$ - Division
$$ a : b = c \quad a, b \in Z,\; c \in Q $$ - Exponentiation
$$ a^b = c \quad a, b \in Z,\; c \in Q $$
Note. Addition, subtraction, and multiplication are internal operations on the set of integers Z, because their results always belong to Z. Division and exponentiation, by contrast, are not internal operations, since their results may fall outside Z. In such cases, the result belongs to the set of rational numbers Q.
Properties of the Integers
The integers satisfy a set of fundamental algebraic properties that govern how addition and multiplication behave. These properties form the foundation of much of elementary and abstract algebra.
- Commutative property of addition
$$ a + b = b + a $$ - Commutative property of multiplication
$$ a \cdot b = b \cdot a $$ - Associative property of addition
$$ (a + b) + c = a + (b + c) $$ - Associative property of multiplication
$$ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$ - Distributive property of multiplication over addition
$$ a(b + c) = ab + ac \quad \text{and} \quad (a + b)c = ac + bc $$ - Additive identity
$$ a + 0 = 0 + a = a $$ - Multiplicative identity
$$ a \cdot 1 = 1 \cdot a = a $$ - Additive inverse
$$ a + (-a) = (-a) + a = 0 $$
In all expressions above, a, b, and c denote arbitrary integers.
Corollaries
Several useful results follow directly from these properties.
-
$$ a \cdot 0 = 0 \cdot a = 0 $$
Proof
Since 0 is the additive identity, we may write $$ a \cdot 0 = a \cdot (0 + 0). $$ Applying the distributive property gives $$ a \cdot (0 + 0) = a \cdot 0 + a \cdot 0. $$ Therefore, $$ a \cdot 0 = a \cdot 0 + a \cdot 0. $$ Subtracting \( a \cdot 0 \) from both sides yields $$ a \cdot 0 = 0. $$ -
$$ (-a) \cdot b = -(a \cdot b) $$
Proof
Since multiplication by zero always gives zero, $$ b \cdot 0 = 0. $$ Because zero can be written as the sum of a number and its additive inverse, we have $$ b \cdot (a + (-a)) = 0. $$ Applying the distributive property yields $$ (b \cdot a) + (b \cdot (-a)) = 0. $$ Moving the first term to the other side, we obtain $$ b \cdot (-a) = -(b \cdot a). $$ Hence, $$ (-a) \cdot b = -(a \cdot b). $$ -
$$ (-a) \cdot (-b) = ab $$
Proof
Using basic algebraic identities, $$ (-a) \cdot (-b) = (-1) \cdot a \cdot (-1) \cdot b = (-1)(-1)ab. $$ Since \( (-1)(-1) = 1 \), it follows that $$ (-a) \cdot (-b) = ab. $$
The Integers as a Commutative Ring
Algebraic structures that satisfy the same axioms as the integers are called rings.
More precisely, the set of integers forms a commutative ring with identity.
What is a commutative ring?
A commutative ring is a ring in which multiplication is commutative.
For any two integers a and b, their product is again an integer.
$$ \forall a, b \in Z,\quad a \cdot b = b \cdot a \in Z $$
Example
Given any two integers a and b, their product belongs to Z.
$$ a \cdot b = b \cdot a \in Z $$
The Integers as an Integral Domain
What is an integral domain?
An integral domain is a commutative ring with no zero divisors.
What is a zero divisor?
A zero divisor is a nonzero element x of a commutative ring for which there exists a nonzero element y such that $$ x \cdot y = 0. $$
The integers contain no zero divisors.
Therefore, the set of integers is an integral domain.
Proof
We must show that the product of two integers is equal to zero if and only if at least one of the factors is zero.
$$ a \cdot b = 0 \quad \text{if and only if} \quad a = 0 \text{ or } b = 0 $$
If both factors are positive, that is, a > 0 and b > 0, then their product is positive.
$$ a \cdot b > 0 \quad \text{if } a > 0 \text{ and } b > 0 $$
If both factors are negative, that is, a < 0 and b < 0, their product is again positive.
$$ a \cdot b > 0 \quad \text{if } a < 0 \text{ and } b < 0 $$
If one factor is positive and the other is negative, then their product is negative.
$$ a \cdot b < 0 \quad \text{if } a > 0 \text{ and } b < 0 $$
From these cases, it follows that the product ab can be zero only if at least one of the factors is zero.
$$ a \cdot b = 0 \quad \text{if and only if} \quad a = 0 \text{ or } b = 0 $$
Therefore, the set of integers has no zero divisors.
This establishes that the set of integers is an integral domain.
Note. The absence of zero divisors is not a property shared by all rings. Some rings do contain zero divisors. For example, the ring Z₁₀ has zero divisors.
