Monomials
A monomial is an algebraic expression consisting of a single term involving only multiplication and powers, where the exponents of the variables are natural numbers.
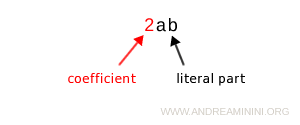
The numerical factor is called the coefficient, while the product of variables is referred to as the literal part of the monomial.
Numerical coefficients may have negative exponents (e.g. $ 4^{-1} = \frac{1}{4} $), but the exponents applied to variables must always be natural numbers (e.g. $ x^0, x^1, x^2, \dots $).
Examples of Monomials
To clarify what qualifies as a monomial - and what does not - let’s look at a few concrete examples.
Here’s a valid example of a monomial:
$$ 2a^3b^4 $$
Here, the coefficient is 2, and the literal part is a3b4.
Note: In a monomial, variable exponents must be natural numbers. If the numerical coefficient is 1 or -1, it's typically omitted, as it's understood implicitly. For example, we write a or -a instead of 1a or -1a.
$$ a \ , \ -a $$
By contrast, the following is not a monomial because it contains two separate terms:
$$ 2a^3 + b^4 $$
This is actually an algebraic sum of monomials, which makes it a polynomial.
Note: The word "monomial" literally means "single term". The expression 2a3 + b4 includes two. The term "monomial" combines the Greek word *monos* (meaning "one") and the Latin *nomen* (meaning "name" or "term").
The next expression also isn't a monomial because one of the variables appears in the denominator, which is equivalent to raising it to a negative exponent:
$$ 2a^3b^{-4} = \frac{2a^3}{b^4} $$
However, this is a monomial, since a numerical coefficient is allowed to have a negative exponent:
$$ 2^{-3}a^3b^4 = \frac{a^3b^4}{2^3} $$
Single variables (like a, b, c, etc.) and single numbers (such as 1, 2, 3, etc.) are also considered monomials.
For instance, a real number is a monomial because it can be viewed as the product of the number and a variable raised to the zero power:
$$ 3 = 3 \cdot a^0 = 3 \cdot 1 $$
Note: This implies that the set of real numbers $ \mathbb{R} $ is a subset of the set of all monomials.
Zero is also considered a monomial. When the coefficient is zero, we refer to it as the zero monomial:
$$ 0 = 0 \cdot a^0 = 0 \cdot 1 $$
Likewise, individual variables are monomials because they can be thought of as the product of 1 and the variable itself:
$$ a = 1 \cdot a $$
These examples should help eliminate any ambiguity about what constitutes a monomial.
Standard Form of a Monomial
A monomial is said to be in standard form when it’s written as the product of a single numerical coefficient and powers of variables, each with a distinct base.
Example
The following expression is not in standard form because the variable "a" appears twice, and there are two separate numerical factors:
$$ 2a^23b^3a $$
To rewrite it in standard form, we group the numerical coefficients and the repeated variables using the commutative and associative properties of multiplication:
$$ (2 \cdot 3) \cdot (a^2 \cdot a) \cdot b^3 $$
Now we compute the product of the numerical coefficients:
$$ 6 (a^2 \cdot a) \cdot b^3 $$
Then we apply the laws of exponents to combine like variables:
$$ 6 (a^{2+1}) \cdot b^3 $$
This gives us the monomial in standard form:
$$ 6 a^3b^3 $$
Degree of a Monomial
The degree of a monomial is the sum of the exponents of all the variables that appear in the expression.
The numerical coefficient is not considered when determining the degree.
A monomial is said to have degree zero if it contains no variables at all.
Note: The zero monomial (i.e., 0) is a special case - it is not assigned a degree.
Example
This monomial has degree 4 because the exponent of "a" is 3 and that of "b" is 1 (3 + 1 = 4):
$$ 2 a^3b $$
Example 2
This monomial has a total degree of 5, since the exponents of the variables "a" and "b" are both 2, and the exponent of "c" is 1 (2 + 2 + 1 = 5).
$$ 2a^2b^2c $$
Example 3
Any non-zero constant has degree zero, as it can be written as the product of itself and a variable raised to the power of zero.
$$ 1 = 1 \cdot x^0 $$
$$ 2 = 2 \cdot x^0 $$
$$ 3 = 3 \cdot x^0 $$
The only exception is zero, whose degree is undefined.
Degree of a Monomial with Respect to a Specific Variable
The degree of a monomial with respect to a particular variable is defined as the exponent of that variable in the monomial's simplified, or standard, form.
To determine the degree with respect to a variable, first rewrite the monomial in standard form by combining like terms, then identify the exponent of the variable in question.
Example
Consider the following monomial:
\( 2x \cdot x^2 \cdot y \)
This expression is not yet in standard form, since powers of the same variable appear multiple times.
Combining the powers of \( x \), we get:
$$ 2x^3y $$
Now we can identify the degrees: the degree with respect to \( x \) is 3, and with respect to \( y \), it is 1.
Note: If a variable does not appear in the monomial, it is understood to have an exponent of zero, and thus a degree of zero with respect to that variable. For instance, in the monomial \( 5x^3y^2 \), the degree with respect to \( z \) is zero, since \( z \) is not present.
Variables and constants in monomials
By default, letters in a monomial are treated as variables.
However, there are cases where a letter represents a fixed value - such as π - in which case it is considered a constant and is not part of the literal part of the monomial.
The literal part consists solely of the product of all the variables. It does not include numerical values or letters that stand for constants.
Constants, even when represented by letters like π, are included in the numerical coefficient of the monomial, as they represent fixed, non-variable quantities.
Example
In the monomial \( \frac{4}{3} \pi r^3 \), which represents the volume of a sphere, π is a constant (approximately 3.14), while \( r \) is a variable (the radius of the sphere).
In this case, the literal part of the monomial is simply \( r^3 \), since π does not vary.
The constant pi (π) is part of the numerical coefficient, which in this case is \( \frac{4}{3} \pi \).
Note. Some constants are universally recognized in mathematics and physics by their standard symbols - for example, pi (π), Euler’s number (e), and so on. In other cases, a constant may be defined within a specific context. To correctly identify the literal part of a monomial, it’s essential to understand what each letter represents: only variables are included in the literal part. For instance, in the monomial \( 7k\alpha^2 \), if \( \alpha \) is known to be a physical constant, then the literal part is simply \( k \). If there’s no such indication, it’s reasonable to treat \( \alpha \) as a variable, making the literal part \( k\alpha^2 \).
And so on.
