Operations with Monomials
The fundamental operations involving monomials
Addition of Monomials
To add two or more monomials with the same literal part (known as like terms), factor out the common variable part and add the numerical coefficients.
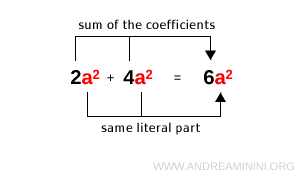
The sum of two monomials is another monomial.
Addition is only possible when the monomials share the exact same literal part - in other words, when they are like terms. Otherwise, the terms cannot be combined.
Example. Consider the sum $$ 2a^3 + 4a^3 $$. Factor the common part: $$ (2 + 4) \cdot a^3 $$. Add the coefficients: $$ 6a^3 $$. This is the algebraic sum of the two monomials.
Example 2. Now consider: $$ 2a^3 + 5a^2 $$. In this case, the literal parts differ, so the expression cannot be simplified and the monomials cannot be added.
You might think that adding two monomials always gives you another monomial - but that’s not necessarily the case.
In fact, addition isn’t a closed operation on monomials. That means the result of adding two monomials isn’t always a monomial itself.
Why? Because only like terms - monomials with the same variables raised to the same powers - can be combined into a single monomial.
If the terms are not like terms, you can’t simplify the expression any further. The result is a polynomial, not a monomial.
Example: $$ 3x^2 + 4x $$ These two terms aren’t like terms, so they can’t be combined. The result is a polynomial with two terms.
Subtraction of Monomials
To subtract two or more monomials with the same literal part (like terms), factor out the common variable part and subtract the numerical coefficients.

The difference of two monomials is also a monomial.
As with addition, subtraction is only possible if the monomials have identical literal parts.
Example. Let’s subtract the monomials $$ 2a^3 - 5a^3 $$ Factor the common part: $$ (2 - 5) \cdot a^3 $$ Subtract the coefficients: $$ -3a^3 $$ This is the algebraic difference of the monomials.
Example 2. Now consider: $$ 2a^3 + 5a^2 $$ Since the literal parts are different, the subtraction is not defined, and the expression cannot be simplified.
Subtracting two like terms can be interpreted as adding the first term to the additive inverse of the second.
Example. To subtract the monomials $$ 2a^3 - 5a^3 $$ we add the first term, $2a^3$, to the opposite of the second term, which is $-5a^3$: $$ (2a^3) - (5a^3) = 2a^3 + (-5a^3) = -3a^3 $$
It’s important to note that subtraction is not a closed operation on monomials, since the result is not necessarily a monomial. If the terms involved are not like terms, the result is a polynomial.
Multiplication of Monomials
The product of two monomials is a monomial whose coefficient is the product of the numerical coefficients and whose literal part is the product of the variable parts.
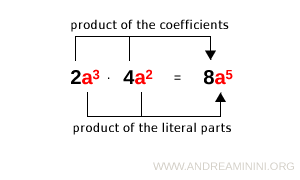
Unlike addition and subtraction, multiplication does not require the monomials to be similar - the variable parts can be different.
To multiply monomials, you must apply the laws of exponents.
Example. Multiply the monomials $$ 4a^2b \cdot 5a^3c $$ Using the associative and commutative properties, group the numerical and literal parts: $$ (4 \cdot 5) \cdot (a^2b \cdot a^3c) $$ Multiply the coefficients: $$ 20 \cdot (a^2b \cdot a^3c) $$ Now combine like bases: $$ 20 \cdot (a^2 \cdot a^3) \cdot b \cdot c $$ Apply the laws of exponents: $$ 20 \cdot a^{2+3} \cdot bc $$ The final product is: $$ 20a^5bc $$
If either of the two monomials is zero, the result is always the zero monomial, since zero is the multiplicative absorbing element - even within the set of monomials.
Example. Consider the product of a monomial and zero: $$ 4a^2b \cdot 0 = (4 \cdot 0) \cdot a^2b = 0 \cdot a^2b = 0 $$
The product of two monomials is always another monomial, which means that multiplication is a closed operation on the set of monomials.
Division of Monomials
The quotient of two monomials is a monomial whose coefficient is the quotient of the numerical coefficients and whose literal part is the quotient of the variable parts. The divisor must not be zero.

As with multiplication, the monomials involved in a division do not need to be similar.
However, it is essential that the divisor is not zero, as division by zero is undefined.
To divide monomials, use the laws of exponents.
Example. Divide the monomials $$ 8a^4b : 4a^3c $$ Rewrite the division as a fraction: $$ \frac{8a^4b}{4a^3c} $$ Group the numerical and literal parts: $$ \frac{8}{4} \cdot \frac{a^4b}{a^3c} $$ Simplify the numerical part: $$ 2 \cdot \frac{a^4b}{a^3c} $$ Now apply the exponent rules: $$ 2 \cdot a^4b \cdot a^{-3}c^{-1} = 2 \cdot a^{4-3}bc^{-1} = 2 \cdot abc^{-1} = \frac{2ab}{c} $$ This is the resulting monomial.
Division is not a closed operation within the set of monomials, as it can produce a result that is no longer a monomial but a rational expression.
For instance, in the division $ \frac{2a^2b}{ac} = \frac{2ab}{c} $, the quotient is not a monomial, but a rational expression.
Raising a Monomial to a Power
Raising a monomial to a power means raising both its coefficient and its literal part to that power.

To raise a monomial to the n-th power, you need to apply the laws of exponents.
This means raising the numerical coefficient to the power of n and multiplying each exponent in the variable part by n.
Example. Raise the monomial $$ (4a^3b)^2 $$ to the second power. Start with the coefficient: $$ 4^2 \cdot (a^3b)^2 = 16 \cdot (a^3b)^2 $$ Now raise the variable part: $$ 16 \cdot a^{3 \cdot 2} \cdot b^2 $$ The result is: $$ 16a^6b^2 $$
Any monomial raised to the zero power is always equal to 1.
$$ (4a^3b)^0 = 4^0 \cdot a^{3 \cdot 0} b^0 = 1 $$
Since the expression $ 0^0 $ is undefined, the zero exponent is not defined for a monomial with a zero coefficient.
Exponentiation is an internal operation on monomials, meaning the result is still a monomial.
And so on.
