Fourier Transform of a Cosine Function
The Fourier Transform of the cosine function in the time domain
$$ x(t) = \cos(2 \pi f_0 t) $$
can be calculated using the integral
$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} \, dt $$
Yet, a faster and simpler approach uses the cosine’s representation with complex exponentials, thanks to Euler’s formula.
$$ x(t) = \cos(2 \pi f_0 t) = \frac{e^{j 2 \pi f_0 t} + e^{-j 2 \pi f_0 t}}{2} $$
This allows us to express the time-domain cosine function \( x(t) = \cos(2 \pi f_0 t) \) as:
$$ x(t) = \frac{1}{2} e^{j 2 \pi f_0 t} + \frac{1}{2} e^{-j 2 \pi f_0 t} $$
Now, we can calculate the Fourier Transform of each term separately.
$$ X(f) = F \left[ \frac{1}{2} e^{j 2 \pi f_0 t} + \frac{1}{2} e^{-j 2 \pi f_0 t} \right] $$
By the linearity property, the Fourier Transform of a sum equals the sum of the individual transforms.
$$ X(f) = F \left[ \frac{1}{2} e^{j 2 \pi f_0 t} \right] + F \left[ \frac{1}{2} e^{-j 2 \pi f_0 t} \right] $$
$$ X(f) = \frac{1}{2} \cdot F \left[ e^{j 2 \pi f_0 t} \right] + \frac{1}{2} \cdot F \left[ e^{-j 2 \pi f_0 t} \right] $$
Referring to the known Fourier Transforms:
- The transform of \( e^{j 2 \pi f_0 t} \) produces a delta function at \( f = f_0 \)
- The transform of \( e^{-j 2 \pi f_0 t} \) produces a delta function at \( f = -f_0 \)
By substituting these results, we obtain the frequency-domain function:
$$ X(f) = \frac{1}{2} \delta(f - f_0) + \frac{1}{2} \delta(f + f_0) $$
where \( \delta(f) \) is the Dirac delta function.
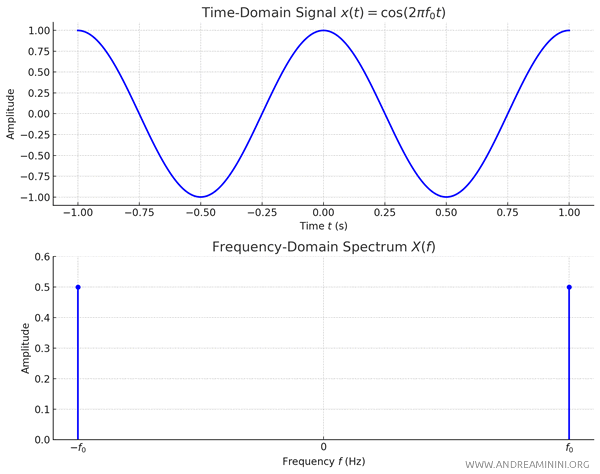
Thus, the Fourier Transform of \( x(t) = \cos(2 \pi f_0 t) \) becomes:
$$ X(f) = \frac{1}{2} \delta(f - f_0) + \frac{1}{2} \delta(f + f_0) $$
This result reveals that the Fourier Transform of a pure cosine function is centered at two distinct frequencies, \( \pm f_0 \).
This approach avoids direct integration by applying known Fourier properties, making the process more efficient and straightforward.
And so forth.
