Fourier Transform of the Sine Function

The Fourier transform of the trigonometric function of the sine in the time domain

$$ x(t) = \sin(2 \pi f_0 t) $$

is computed by evaluating the Fourier integral

$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} \, dt $$

However, it’s far simpler to express the sine function using complex exponentials, utilizing Euler's formula:

$$ x(t) = \sin(2 \pi f_0 t) = \frac{e^{j 2 \pi f_0 t} - e^{-j 2 \pi f_0 t}}{2j} $$

Consequently, I can rewrite $ x(t) = \sin(2 \pi f_0 t) $ as:

$$ x(t) = \frac{1}{2j} e^{j 2 \pi f_0 t} - \frac{1}{2j} e^{-j 2 \pi f_0 t} $$

Next, I will compute the Fourier transform of each term separately:

$$ X(f) = F \left[ \frac{1}{2j} e^{j 2 \pi f_0 t} - \frac{1}{2j} e^{-j 2 \pi f_0 t} \right] $$

Thanks to the linearity of the Fourier transform, I can express this as

$$ X(f) = \frac{1}{2j} \cdot F \left[ e^{j 2 \pi f_0 t} \right] - \frac{1}{2j} \cdot F \left[ e^{-j 2 \pi f_0 t} \right] $$

From known Fourier transforms, I can assert that:

The transform of $ e^{j 2 \pi f_0 t} $ corresponds to an impulse at $ f = f_0 $,
The transform of $ e^{-j 2 \pi f_0 t} $ corresponds to an impulse at $ f = -f_0 $.

Thus, substituting these results yields the Fourier transform of $ x(t) = \sin(2 \pi f_0 t) $ as:

$$ X(f) = \frac{1}{2j} \delta(f - f_0) - \frac{1}{2j} \delta(f + f_0) $$

In conclusion, the Fourier transform of the sine function is represented as the difference of two impulses located at frequencies $ \pm f_0 $, with an imaginary factor of $ \frac{1}{2j} $ that reflects its sinusoidal nature.

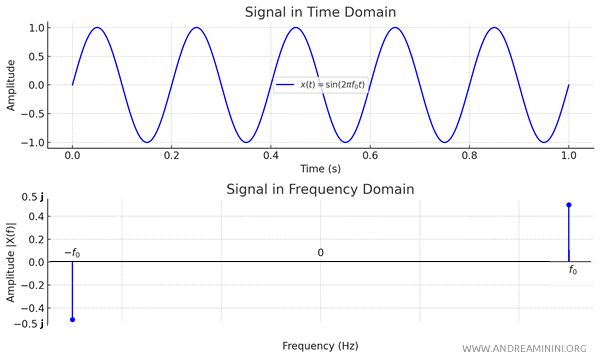
the diagram in time and frequency

This expression illustrates how the energy of the sine function concentrates at frequencies $ \pm f_0 $ in the frequency domain, but with a different phase compared to the cosine function.

And so forth.